Question

【题目】已知椭圆C1： 的离心率为 ，焦距为 ，抛物线C2：x2=2py（p＞0）的焦点F是椭圆C1的顶点． （Ⅰ）求C1与C2的标准方程；
（Ⅱ）C1上不同于F的两点P，Q满足 ，且直线PQ与C2相切，求△FPQ的面积．

Answer 1

【答案】解：（Ⅰ）设椭圆C1的焦距为2c，依题意有 ， ， 解得 ，b=2，故椭圆C1的标准方程为 ．
又抛物线C2：x2=2py（p＞0）开口向上，故F是椭圆C1的上顶点，
∴F（0，2），∴p=4，
故抛物线C2的标准方程为x2=8y．…（5分）
（Ⅱ）由题意得直线PQ的斜率存在．设直线PQ的方程为y=kx+m，
设P（x1 ， y1），Q（x2 ， y2），则 ， ，
∴ ，
即 （*）
联立 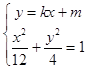，消去y整理得，（3k2+1）x2+6kmx+3m2﹣12=0（**）．
依题意，x1 ， x2是方程（**）的两根，△=144k2﹣12m2+48＞0，
∴ ， ，
将x1+x2和x1x2代入（*）得m2﹣m﹣2=0，
解得m=﹣1，（m=2不合题意，应舍去）．
联立 ，消去y整理得，x2﹣8kx+8=0，
令△'=64k2﹣32=0，解得 ．
经检验， ，m=﹣1符合要求．
此时， ，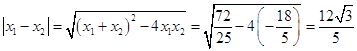
∴
【解析】（Ⅰ）设椭圆C1的焦距为2c，依题意有 ， ，由此能求出椭圆C1的标准方程；又抛物线C2：x2=2py（p＞0）开口向上，故F是椭圆C1的上顶点，由此能求出抛物线C2的标准方程．（Ⅱ）设直线PQ的方程为y=kx+m，设P（x1 ， y1），Q（x2 ， y2），则 ， ，联立 ，得（3k2+1）x2+6kmx+3m2﹣12=0，由此利用根的判别式、韦达定理、弦长公式，结合已知件能求出△FPQ的面积．