题目内容
已知数列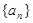 ,
, 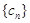 满足条件:
满足条件: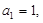
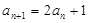 ,
, 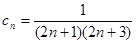 .
.
(1)求证数列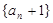 是等比数列,并求数列
是等比数列,并求数列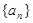 的通项公式;
的通项公式;
(2)求数列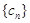 的前
的前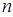 项和
项和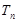 ,并求使得
,并求使得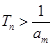 对任意
对任意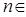 N*都成立的正整数
N*都成立的正整数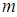 的最小值.
的最小值.
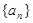 ,
, 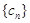 满足条件:
满足条件: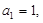
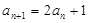 ,
, 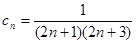 .
.(1)求证数列
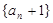 是等比数列,并求数列
是等比数列,并求数列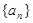 的通项公式;
的通项公式;(2)求数列
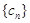 的前
的前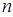 项和
项和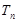 ,并求使得
,并求使得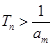 对任意
对任意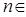 N*都成立的正整数
N*都成立的正整数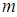 的最小值.
的最小值.(1) (2)正整数
(2)正整数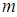 的最小值是5
的最小值是5
 (2)正整数
(2)正整数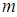 的最小值是5
的最小值是5试题分析:(1)由数列的递推公式求数列的通项公式,根据等比数列的定义,只要证明
 即可
即可(2)由
 ,利用裂项相消法,可得
,利用裂项相消法,可得 ,
,然后证明数列
 是一个递增数列,当
是一个递增数列,当 时,
时,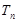 取得最小值
取得最小值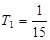 ,要使得
,要使得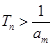 对任意
对任意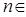 N*都成立,结合(1)的结果,只需
N*都成立,结合(1)的结果,只需 ,解之即可
,解之即可(1)∵
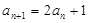
∴
 ,∵
,∵ ,
,
∴数列
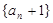 是首项为2,公比为2的等比数列 .
是首项为2,公比为2的等比数列 .∴
 ∴
∴
(2)∵
 ,
,∴

 .
.∵
 ,又
,又 ,
,∴
 N*,即数列
N*,即数列 是递增数列.
是递增数列. ∴当
 时,
时,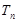 取得最小值
取得最小值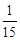 .
.要使得
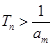 对任意
对任意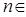 N*都成立,结合(1)的结果,只需
N*都成立,结合(1)的结果,只需 ,由此得
,由此得 .∴正整数
.∴正整数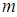 的最小值是5.
的最小值是5.
练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
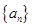 的前
的前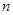 项和
项和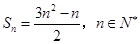 .
.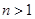 ,都有
,都有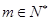 ,使得
,使得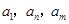 成等比数列.
成等比数列. 中,
中, ,公比
,公比 ,用
,用 表示它的前n项之积,则
表示它的前n项之积,则

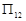

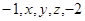 成等比数列,则
成等比数列,则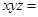 ( )
( )



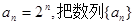 的各项排成如右侧三角形状,记
的各项排成如右侧三角形状,记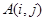 表示第
表示第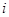 行中第
行中第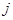 个数,则结论
个数,则结论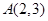 =16;
=16; 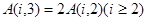 ;
;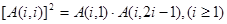 ;
;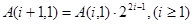 ;其中正确的是 (写出所有正确结论的序号).
;其中正确的是 (写出所有正确结论的序号). 中,若
中,若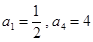 ,则公比
,则公比