Question

【题目】已知椭圆C：（）的两焦点与短轴的一个端点的连线构成等腰直角三角形，直线与以椭圆C的右焦点为圆心，以椭圆的半长轴长为半径的圆相切．

（1）求椭圆C的方程；

（2）设P为椭圆C上一点，若过点的直线l与椭圆C相交于不同的两点S和T，满足（O为坐标原点），求实数t的取值范围．

Answer 1

【答案】（1）；（2）．

【解析】

（1）根据题意设出圆的标准方程，利用切线的性质、等腰直角三角形的性质，结合椭圆中的关系进行求解即可；

（2）根据题意设出直线l的方程和点P的坐标，将直线与椭圆的方程联立，根据直线与椭圆的位置关系，结合一元二次根的判别式、根与系数的关系、平面向量加法和数乘的坐标表示公式进行求解即可.

（1）由题意，以椭圆C的右焦点为圆心，以椭圆的长半轴长为半径的圆的方程为

，∴圆心到直线的距离为（*）

∵椭圆C的两焦点与短轴的一个端点的连线构成等腰直角三角形，

∴，

代入（*）式得，∴，

故所求椭圆方程为

（2）由题意知直线l的斜率存在，设直线l方程为，设，

将直线方程代入椭圆方程得，

，，

设，，则，

由，

当时，直线l为x轴，P点在椭圆上适合题意；

当时，得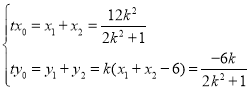

∴，

将上式代入椭圆方程得：，

整理得：，

由知，所以，∴

综上可得