题目内容
【题目】已知抛物线
的焦点为
，准线为
，抛物线
上存在一点
，过点作
，垂足为
，使
是等边三角形且面积为
.
（1）求抛物线的方程；
（2）若点
是圆
与抛物线的一个交点，点
，当
取得最小值时，求此时圆
的方程.
【答案】（1）
（2）
【解析】
（1）利用等边三角形可得
值，从而得到抛物线
的方程；
（2）设
的坐标为
，易得
，所以
，结合最值即可得到圆
的方程.
解：（1）如图所示，
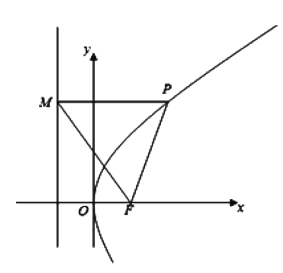
∵等边
的面积为
，
设边长为
，
∴
，∴
，∴
∵
，∴
所以抛物线的方程是.
（2）法一：设的坐标为，因为抛物线：的焦点
，
，
，
所以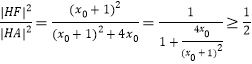
当且仅当
时取等号，即当
取最小值时，点坐标为
把点坐标代入圆的方程可得.
法二：设的坐标为
，因为抛物线：的焦点，
，
，
所以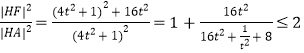
，当且仅当
时取等号，
即当取最小值时，点坐标为
把点坐标代入圆的方程可得.
导学与测试系列答案
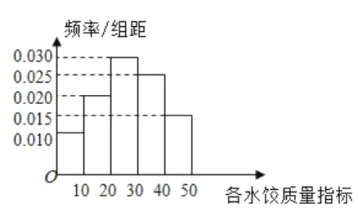
新非凡教辅冲刺100分系列答案【题目】在2018年俄罗斯世界杯期间,莫斯科的部分餐厅经营了来自中国的小龙虾,这些小龙虾标有等级代码.为得到小龙虾等级代码数值
与销售单价
之间的关系,经统计得到如下数据：
等级代码数值 | 38 | 48 | 58 | 68 | 78 | 88 |
销售单价 | 16.8 | 18.8 | 20.8 | 22.8 | 24 | 25.8 |
（1）已知销售单价与等级代码数值之间存在线性相关关系,求关于的线性回归方程(系数精确到0.1)；
（2）若莫斯科某餐厅销售的中国小龙虾的等级代码数值为98，请估计该等级的中国小龙虾销售单价为多少元？
参考公式：对一组数据
,
，····
,其回归直线
的斜率和截距最小二乘估计分别为：
,
.
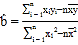参考数据：
,
.
【题目】某种植物感染
病毒极易导致死亡，某生物研究所为此推出了一种抗病毒的制剂，现对20株感染了病毒的该植株样本进行喷雾试验测试药效.测试结果分“植株死亡”和“植株存活”两个结果进行统计；并对植株吸收制剂的量(单位：mg)进行统计.规定：植株吸收在6mg（包括6mg）以上为“足量”，否则为“不足量”.现对该20株植株样本进行统计，其中 “植株存活”的13株，对制剂吸收量统计得下表.已知“植株存活”但“制剂吸收不足量”的植株共1株.
编号 | 01 | 02 | 03 | 04 | 05 | 06 | 07 | 08 | 09 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
吸收量(mg) | 6 | 8 | 3 | 8 | 9 | 5 | 6 | 6 | 2 | 7 | 7 | 5 | 10 | 6 | 7 | 8 | 8 | 4 | 6 | 9 |
（1）完成以下
列联表，并判断是否可以在犯错误概率不超过1%的前提下，认为“植株的存活”与“制剂吸收足量”有关？
吸收足量 | 吸收不足量 | 合计 | |
植株存活 | 1 | ||
植株死亡 | |||
合计 | 20 |
（2）①若在该样本“吸收不足量”的植株中随机抽取3株，记
为“植株死亡”的数量，求得分布列和期望
；
②将频率视为概率，现在对已知某块种植了1000株并感染了病毒的该植物试验田里进行该药品喷雾试验，设“植株存活”且“吸收足量”的数量为随机变量
，求
.
参考数据：
，其中
