题目内容
【题目】建造一条防洪堤,其断面为等腰梯形,腰与底边成角为![]() ,防洪堤高记为
,防洪堤高记为![]() (如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为![]() 平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长
平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长![]() (
(![]() )要最小.
)要最小.

(1)用![]() 表示
表示![]() 、
、![]() ;
;
(2)将![]() 表示成
表示成![]() 的函数
的函数![]() ,如
,如![]() 限制在
限制在![]() 范围内,
范围内,![]() 最小为多少米?并说明理由.
最小为多少米?并说明理由.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() 的最小值为
的最小值为![]() .
.
【解析】
(1)在直角三角形中,利用正弦函数即可求得![]() ,再利用梯形的面积,求得
,再利用梯形的面积,求得![]() .
.
(2)利用(1)中的结论,即可得到函数的解析式,再根据对勾函数的单调性即可求得函数的最小值.
(1)在直角三角形![]() 中,由
中,由![]() ,
,
可得![]() ,
,![]()
设![]() ,故
,故![]()
由梯形的面积可得:![]()
即
解得![]()
综上所述:![]() ,
,![]() .
.
(2)因为![]()
故可得![]()
下证:函数![]() 在
在![]() 是单调递增函数.
是单调递增函数.
任取![]()
则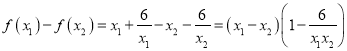
因为![]() ,故
,故![]() ;又
;又![]() ,故
,故![]() ,则
,则![]()
故![]() ,即
,即![]() ,
,
故函数![]() 在区间
在区间![]() 上单调递增.
上单调递增.
因为![]()
![]() ,函数
,函数![]() 单调递增,
单调递增,
故![]() .
.

练习册系列答案
相关题目
【题目】某同学的父亲决定今年夏天卖西瓜赚钱,根据去年6月份的数据统计连续五天内每天所卖西瓜的个数与温度之间的关系如下表:
温度 | 32 | 33 | 35 | 37 | 38 |
西瓜个数 | 20 | 22 | 24 | 30 | 34 |
(1)求这五天内所卖西瓜个数的平均值和方差;
(2)求变量![]() 之间的线性回归方程,并预测当温度为
之间的线性回归方程,并预测当温度为![]() 时所卖西瓜的个数.
时所卖西瓜的个数.
附: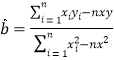 ,
,![]() (精确到
(精确到![]() ).
).