题目内容
【题目】已知等差数列![]() 中,公差
中,公差![]() ,其前
,其前![]() 项和为
项和为![]() ,且满足:
,且满足:![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
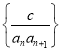
(Ⅱ)通过公式![]() 构造一个新的数列
构造一个新的数列![]() .若
.若![]() 也是等差数列,求非零常数
也是等差数列,求非零常数![]() ;
;
(Ⅲ)求![]() 的最大值.
的最大值.
【答案】(I)![]() ;(II)
;(II)![]() ;(III)
;(III)![]()
【解析】
试题
(1)由等差数列的性质可得a2+a3=14,解方程组可得a2=5,a3=9,于是可求得首项和公差,从而可得通项公式.(2)由题意得Sn=2n2-n,故![]() ,根据数列为等差数列可得2b2=b1+b3,计算可得
,根据数列为等差数列可得2b2=b1+b3,计算可得![]() .经验证可得
.经验证可得![]() 满足题意.(3)由(2)可得
满足题意.(3)由(2)可得 ,故可根据基本不等式求最值.
,故可根据基本不等式求最值.
试题解析:
(1)∵数列{an}是等差数列.
∴a2+a3=a1+a4=14,
由 ,解得
,解得 或
或 .
.
∵公差d>0,
∴a2=5,a3=9.
∴d=a3-a2=4,a1=a2-d=1.
∴![]() .
.
(2)∵Sn=na1+![]() n(n-1)d=n+2n(n-1)=2n2-n,
n(n-1)d=n+2n(n-1)=2n2-n,
∴![]() .
.
∵数列{bn}是等差数列,
∴2b2=b1+b3,
∴2·![]() =
=![]() +
+![]() ,
,
解得![]() (c=0舍去).
(c=0舍去).
∴ .
.
显然{bn}成等差数列,符合题意,
∴![]() .
.
(3)由(2)可得
 ,当且仅当
,当且仅当![]() ,即
,即![]() 时等号成立.
时等号成立.
∴f(n)的最大值为![]() .
.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案【题目】某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,续保人的本年度的保费与其上年度的出险次数的关联如下:
(单位:元),继续购买该险种的投保人称为续保人,续保人的本年度的保费与其上年度的出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 |
|
保费 |
|
|
|
|
|
|
设该险种一续保人一年内出险次数与相应概率如下:
一年内出险次数 | 0 | 1 | 2 | 3 | 4 |
|
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
(Ⅰ)求一续保人本年度的保费高于基本保费的概率;
(Ⅱ)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出![]() 的概率;
的概率;
(Ⅲ)求续保人本年度的平均保费与基本保费的比值.
【题目】在一段时间内,分5次测得某种商品的价格x(万元)和需求量y(t)之间的一组数据为:
1 | 2 | 3 | 4 | 5 | |
价格x | 1.4 | 1.6 | 1.8 | 2 | 2.2 |
需求量y | 12 | 10 | 7 | 5 | 3 |
已知![]() ,
,
(1)画出散点图;
(2)求出y对x的线性回归方程;
(3)如价格定为1.9万元,预测需求量大约是多少?(精确到0.01 t).
参考公式: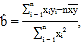
![]() .
.