Question

【题目】如图，四棱锥P﹣ABCD中，底面ABCD是边长为2的菱形，∠DAB＝60°，AC∩BD＝O，点P在底面的射影为点O，PO＝3，点E为线段PD中点．

（1）求证：PB∥平面AEC；

（2）若点F为侧棱PA上的一点，当PA⊥平面BDF时，试确定点F的位置，并求出此时几何体F﹣BDC的体积．

Answer 1

【答案】（1）见解析（2）F为AP的四等分点（靠近A），几何体F﹣BDC的体积为

【解析】

（1）连接OE，利用中位线知识即可证得：PB∥OE，问题得证。

（2）利用PO⊥平面ABCD证得：BD⊥PA，作BF⊥PA交PA于F，连接DF，即可证得：PA⊥平面BDF，利用等面积法可得OF，结合已知可得：F为AP的四等分点（靠近A），利用体积转化可得：VF﹣BDC，再利用锥体体积公式计算得解。

解：

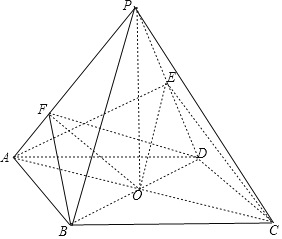
（1）证明：连接OE，

∵O，E为BD，PD的中点，

∴PB∥OE，

又PB平面AEC，OE平面AEC，

∴PB∥平面AEC；

（2）∵PO⊥平面ABCD，

∴PO⊥BD，

又BD⊥AC，

∴BD⊥平面PAC，

∴BD⊥PA，

作BF⊥PA交PA于F，连接DF，

则PA⊥平面BDF，

在菱形ABCD中，∠DAB＝60°，边长为2，

可求得AO，

在Rt△POA中，求得PA，

连接OF，易知PA⊥OF，

利用等面积法可得OF，

在Rt△AFO中，求得AF，

即F为AP的四等分点（靠近A），

∴VF﹣BDC

．

故几何体F﹣BDC的体积为．