Question

【题目】如图,在四棱锥P-ABCD中,四边形ABCD是矩形,E,M分别是AD,PD的中点,PE⊥BE,PA=PD=AD=2,AB=.

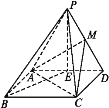
(1)求证:PB∥平面MAC.

(2)求证:平面MAC⊥平面PBE.

Answer 1

【答案】（1）见解析；（2）见解析

【解析】分析：（1）利用三角形的中位线性质得到线线平行，再利用线面平行的判定定理进行证明；（2）利用等边三角形的“三线合一”证得线线垂直，再利用线面垂直的判定定理和性质得到线面垂直和线线垂直，再利用线面垂直和面面垂直的判定定理进行证明．

详解：(1)连接BD交线段AC于点N,连接MN,则N为线段BD中点.

∵点M为线段PD中点,∴MN∥PB.又∵MN平面MAC,PB平面MAC,

∴PB∥平面MAC.

(2)∵PA=PD=AD=2,∴三角形PAD为等边三角形.

又∵E为AD中点,∴PE⊥AD.又∵PE⊥BE,BE∩AD=E,

∴PE⊥平面ABCD.又∵AC平面ABCD,∴AC⊥PE.

∵AD=2,AB=,四边形ABCD是矩形,E是AD中点,

∴△ABE∽△DAC,∴∠ABE=∠DAC,∴AC⊥BE.

∵PE∩BE=E,∴AC⊥平面PBE.∵AC平面MAC,

∴平面MAC⊥平面PBE.