题目内容
【题目】某颜料公司生产A，B两种产品，其中生产每吨A产品，需要甲染料1吨，乙染料4吨，丙染料2吨，生产每吨B产品，需要甲染料1吨，乙染料0吨，丙染料5吨，且该公司一条之内甲、乙、丙三种染料的用量分别不超过50吨、160吨和200吨，如果A产品的利润为300元/吨，B产品的利润为200元/吨，则该颜料公司一天之内可获得的最大利润为 ．
【答案】14000元
【解析】解：设该公司每天生产A产品x钝，生产B产品y钝，则一天的利润为z=300x+200y， 其中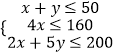 
，
作出平面区域如图所示：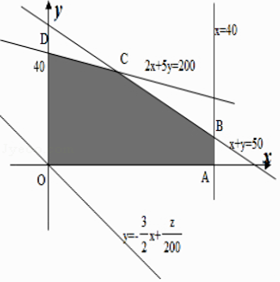
由z=300x+200y得y=﹣ 
+ 
，
由图象可知直线y=﹣ + 经过点B时，直线截距最大，此时z最大．
解方程组 
得 
，
∴z的最大值为300×40+200×10=14000．
所以答案是：14000元．
【考点精析】认真审题，首先需要了解基本不等式在最值问题中的应用(用基本不等式求最值时（积定和最小，和定积最大），要注意满足三个条件“一正、二定、三相等”)．
练习册系列答案
阅读快车系列答案
相关题目
【题目】保险公司统计的资料表明：居民住宅区到最近消防站的距离x（单位：千米）和火灾所造成的损失数额y(单位：千元)有如下的统计资料：
距消防站距离x（千米） | 1.8 | 2.6 | 3.1 | 4.3 | 5.5 | 6.1 |
火灾损失费用y（千元） | 17.8 | 19.6 | 27.5 | 31.3 | 36.0 | 43.2 |
如果统计资料表明y与x有线性相关关系，试求：
（Ⅰ）求相关系数
（精确到0.01）；
（Ⅱ）求线性回归方程（精确到0.01）；
（III）若发生火灾的某居民区与最近的消防站相距10.0千米，评估一下火灾的损失（精确到0.01）.
参考数据：
，
，
，
，
，
参考公式：相关系数 
，回归方程
中斜率和截距的最小二乘估计公式分别为：
，
