题目内容
4.已知函数f(x)=alnx+$\frac{{x}^{2}}{2}$-(a+1)x,a∈R.当a=-1时,求函数f(x)的最小值.分析 当a=-1时,f(x)=-lnx+$\frac{1}{2}$x2的定义域为(0,+∞),再求导,通过导数的正负确定函数的单调性,从而求最小值.
解答 解:当a=-1时,f(x)=-lnx+$\frac{1}{2}$x2的定义域为(0,+∞),
f′(x)=-$\frac{1}{x}$+x=$\frac{(x+1)(x-1)}{x}$,
故f(x)在(0,1)上单调递减,在(1,+∞)上单调递增;
故当x=1时,函数f(x)取得极小值,且为最小值f(1)=$\frac{1}{2}$.
点评 本题考查导数的运用:求单调区间和极值、最值,考查运算能力,属于中档题.

练习册系列答案
相关题目
12.已知α∥β,λ∩β=b,λ∩α=a,那么a与b的关系是( )
| A. | 平行 | B. | 相交 | C. | 异面 |
16.抛掷一颗骰子得到的点数记为m,对于函数f(x)=sinπx,则“y=f(x)在[0,m]上至少有5个零点”的概率是( )
| A. | $\frac{5}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
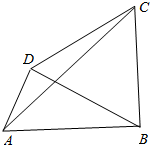 如图,四边形ABCD中,AB=2,AD=1,三角形BCD为正三角形.
如图,四边形ABCD中,AB=2,AD=1,三角形BCD为正三角形. 如图所示的一个算法,其作用是输入x的值,输出相应y的值,若要使输出的y的值为正数,求输入的x值的取值范围.
如图所示的一个算法,其作用是输入x的值,输出相应y的值,若要使输出的y的值为正数,求输入的x值的取值范围.