题目内容
17.数列{an}满足a1=1,an=$\frac{1}{2}$an-1+1(n≥2).(1)若bn=an-2,求证:{bn}为等比数列;
(2)求{an}的通项公式;
(3)求{an}的前n项和Sn.
分析 (1)利用$\frac{{b}_{n+1}}{{b}_{n}}$=$\frac{{a}_{n+1}-2}{{a}_{n}-2}$=$\frac{\frac{1}{2}{a}_{n}+1-2}{{a}_{n}-2}$计算即得结论;
(2)通过bn=-$\frac{1}{{2}^{n-1}}$,即得结论;
(3)通过an=2-$\frac{1}{{2}^{n-1}}$,计算即得结论.
解答 (1)证明:∵a1=1,an=$\frac{1}{2}$an-1+1(n≥2),
∴an≠2,即bn≠0,
∴$\frac{{b}_{n+1}}{{b}_{n}}$=$\frac{{a}_{n+1}-2}{{a}_{n}-2}$=$\frac{\frac{1}{2}{a}_{n}+1-2}{{a}_{n}-2}$=$\frac{\frac{1}{2}({a}_{n}-2)}{{a}_{n}-2}$=$\frac{1}{2}$,
又∵a1=1,∴b1=a1-2=-1,
∴数列{bn}是以-1为首项、$\frac{1}{2}$为公比的等比数列;
(2)解:∵bn=-1•$\frac{1}{{2}^{n-1}}$=-$\frac{1}{{2}^{n-1}}$,
∴an=2+bn=2-$\frac{1}{{2}^{n-1}}$;
(3)解:∵an=2-$\frac{1}{{2}^{n-1}}$,
∴Sn=2n-($\frac{1}{{2}^{0}}$+$\frac{1}{{2}^{1}}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n-1}}$)
=2n-$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$
=2n-$\frac{{2}^{n}-1}{{2}^{n-1}}$.
点评 本题考查数列的通项及前n项和,考查运算求解能力,注意解题方法的积累,属于中档题.

| A. | $\frac{3}{2}$ | B. | $\frac{3}{2}$或0 | C. | -$\frac{2}{3}$ | D. | -$\frac{2}{3}$或0 |
| A. | 平行 | B. | 相交 | C. | 异面 |

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
 某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数,按十位数字为茎,个位数字为叶得到的茎叶图如图所示.已知甲、乙两组数据的平均数都为10.
某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数,按十位数字为茎,个位数字为叶得到的茎叶图如图所示.已知甲、乙两组数据的平均数都为10.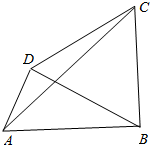 如图,四边形ABCD中,AB=2,AD=1,三角形BCD为正三角形.
如图,四边形ABCD中,AB=2,AD=1,三角形BCD为正三角形.