题目内容
14.已知数列{an}满足a1=1,a2=4,an+2=3an+1-2an(n∈N*).(1)设bn=an+1-2an,证明数列{bn}既是等差数列又是等比数列;
(2)求数列{an}的通项公式.
分析 (1)通过对an+2=3an+1-2an(n∈N*)变形可知an+2-2an+1=an+1-2an(n∈N*),进而可得结论;
(2)通过a1=1、a2=4、an+2-2an+1=an+1-2an(n∈N*)可知an+1-2an=2,进而an+1+2=2(an+2),进而计算可得结论.
解答 (1)证明:∵an+2=3an+1-2an(n∈N*),
∴an+2-2an+1=an+1-2an(n∈N*),
即bn+1=bn,
∴数列{bn}既是等差数列又是等比数列;
(2)解:∵a1=1,a2=4,
∴a2-2a1=4-2=2,
又∵an+2-2an+1=an+1-2an(n∈N*),
∴an+1-2an=2,
即an+1+2=2(an+2),
又∵a1+2=1+2=3,
∴an+2=3•2n-1,
∴an=-2+3•2n-1.
点评 本题考查数列的通项及等差、等比数列的判定,考查运算求解能力,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
6.若某程序框图如图所示,当输入50时,则该程序运算后输出的结果是( )


| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
4.具有线性相关关系的变量x,y,满足一组数据如下表所示:
若y与x的回归直线方程为$\widehat{y}$=3x-$\frac{3}{2}$,则m的值是4.
| X | 0 | 1 | 2 | 3 |
| y | -1 | 1 | m | 8 |
 某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数,按十位数字为茎,个位数字为叶得到的茎叶图如图所示.已知甲、乙两组数据的平均数都为10.
某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数,按十位数字为茎,个位数字为叶得到的茎叶图如图所示.已知甲、乙两组数据的平均数都为10.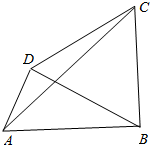 如图,四边形ABCD中,AB=2,AD=1,三角形BCD为正三角形.
如图,四边形ABCD中,AB=2,AD=1,三角形BCD为正三角形.