题目内容
20.已知角α的终边在直线3x+y=0上,求sin2α+sinα•cosα-2cos2α.分析 利用三角函数的定义求出α的正弦和余弦值,代入的计算.
解答 解:因为角α的终边在直线3x+y=0上,取点(1,-3)得到sinα=$\frac{-3}{\sqrt{10}}$,cosα=$\frac{1}{\sqrt{10}}$,
所以sin2α+sinα•cosα-2cos2α=$\frac{9}{10}+\frac{-3}{10}-2×\frac{1}{10}$=$\frac{2}{5}$.
点评 本题考查了三角函数的坐标法定义;关键是由已知角α的终边在直线3x+y=0上求出α的正弦和余弦值.

练习册系列答案
相关题目
6.在△ABC中,角A,B,C所对的边分别为a,b,c,且a=10,b=8,B=30°,那么△ABC的解的情况是( )
| A. | 无解 | B. | 一解 | C. | 两解 | D. | 一解或两解 |
12.已知α∥β,λ∩β=b,λ∩α=a,那么a与b的关系是( )
| A. | 平行 | B. | 相交 | C. | 异面 |
10.复数z满足|z-i|+|z+3|=10,则复数z对应点的集合表示的图形是( )
| A. | 直线 | B. | 圆 | C. | 椭圆 | D. | 双曲线 |
 某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数,按十位数字为茎,个位数字为叶得到的茎叶图如图所示.已知甲、乙两组数据的平均数都为10.
某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数,按十位数字为茎,个位数字为叶得到的茎叶图如图所示.已知甲、乙两组数据的平均数都为10.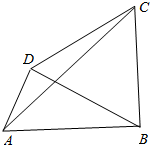 如图,四边形ABCD中,AB=2,AD=1,三角形BCD为正三角形.
如图,四边形ABCD中,AB=2,AD=1,三角形BCD为正三角形.