题目内容
19.已知a>0,函数f(x)=lnx+$\frac{1}{ax}$在[1,+∞)上是增函数,实数a的取值范围是[1,+∞).分析 问题转化为ax-1≥0在[1,+∞)恒成立,结合函数的单调性,从而求出答案.
解答 解:f′(x)=$\frac{1}{x}$-$\frac{1}{{ax}^{2}}$=$\frac{ax-1}{{ax}^{2}}$,
若函数f(x)=lnx+$\frac{1}{ax}$在[1,+∞)上是增函数,(a>0),
则ax-1≥0在[1,+∞)恒成立,即:a≥${(\frac{1}{x})}_{max}$=1,
故答案为:[1,+∞).
点评 本题考查了函数恒成立问题,考查导数的应用,是一道基础题.

练习册系列答案
相关题目
10.复数z满足|z-i|+|z+3|=10,则复数z对应点的集合表示的图形是( )
| A. | 直线 | B. | 圆 | C. | 椭圆 | D. | 双曲线 |
4.具有线性相关关系的变量x,y,满足一组数据如下表所示:
若y与x的回归直线方程为$\widehat{y}$=3x-$\frac{3}{2}$,则m的值是4.
| X | 0 | 1 | 2 | 3 |
| y | -1 | 1 | m | 8 |
9.下列算法语句的处理功能是( )
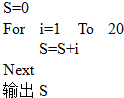
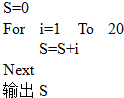
| A. | S=1+2+3+…+20 | B. | S=1+2+3+…+19 | C. | S=2+3+…+20 | D. | S=2+3+…+19 |
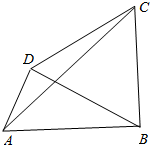 如图,四边形ABCD中,AB=2,AD=1,三角形BCD为正三角形.
如图,四边形ABCD中,AB=2,AD=1,三角形BCD为正三角形. 如图所示的一个算法,其作用是输入x的值,输出相应y的值,若要使输出的y的值为正数,求输入的x值的取值范围.
如图所示的一个算法,其作用是输入x的值,输出相应y的值,若要使输出的y的值为正数,求输入的x值的取值范围.