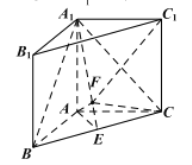
题目内容

【题目】如图所示，ABCD－A1B1C1D1是长方体，O是B1D1的中点，直线A1C交平面AB1D1于点M，则下列结论正确是( )

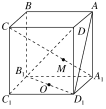
A.A，M，O三点共线B.A，M，O，A1不共面

C.A，M，C，O不共面D.B，B1，O，M共面

【答案】A

【解析】

本题利用直接法进行判断，先观察图形判断A，M，O三点共线，为了要证明A，M，O三点共线，先将M看成是在平面ACC1A1与平面AB1D1的交线上，利用同样的方法证明点O、A也是在平面ACC1A1与平面AB1D1的交线上，从而证明三点共线．

连接A1C1，AC，则A1C1∥AC，

∴A1，C1，A，C四点共面，

∴A1C平面ACC1A1，

∵M∈A1C，∴M∈平面ACC1A1，又M∈平面AB1D1，

∴M在平面ACC1A1与平面AB1D1的交线上，

同理O在平面ACC1A1与平面AB1D1的交线上．

∴A，M，O三点共线．

故选：A．

练习册系列答案
相关题目

【题目】设点，分别是椭园C：的左、右焦点，且椭圆C上的点到的距离的最小值为，点M，N是椭圆C上位于x轴上方的两点，且向量与向量平行．

求椭圆C的方程；

当时，求的面积；

当时，求直线的方程．

【题目】老况、老王、老顾、小周、小郭和两位王女士共7人要排成一排拍散伙纪念照.

（1）若两位王女士必须相邻，则共有多少种排队种数？

（2）若老王与老况不能相邻，则共有多少种排队种数？

（3）若两位王女士必须相邻，若老王与老况不能相邻，小郭与小周不能相邻，则共有多少种排队种数？

【题目】已知动点E到点A（2，0）与点B（-2，0）的直线斜率之积为-，点E的轨迹为曲线C．

（1）求曲线C的方程；

（2）过点D（l，0）作直线l与曲线C交于P，Q两点，且=-．求直线l的方程．

【题目】在某些竞赛活动中，选手的最终成绩是将前面所有轮次比赛成绩求算术平均获得的.同学们知道这样一个事实：在所有轮次的成绩中，如果由高到低依次去掉一些高分，那么平均分降低；反之，如果由低到高依次去掉一些低分，那么平均分提高. 这两个事实可以用数学语言描述为：若有限数列满足，且不全相等，则(1)_______；(2)_______．

【题目】如图，已知直三棱柱中，，，是的中点，是上一点，且.

（1）证明：平面；

（2）求二面角余弦值的大小.

【题目】已知函数，.

（Ⅰ）若，求实数取值的集合；

（Ⅱ）当时，对任意，，令，证明.

【题目】选修4-4：坐标系与参数方程

在直角坐标系中，直线的参数方程为(为参数,倾斜角),曲线C的参数方程为(为参数,)，以坐标原点为极点，轴正半轴为极轴建立极坐标系。

（1）写出曲线的普通方程和直线的极坐标方程;

（2）若直线与曲线恰有一个公共点，求点的极坐标。

【题目】如图，是圆的直径，垂直圆所在的平面，是圆上的一点.

（1）求证：平面 平面；

（2）若，求直线与平面所成角的正弦值.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网