题目内容
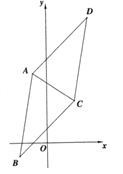
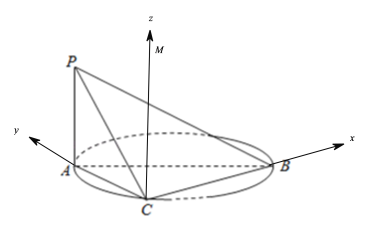
【题目】如图,![]() 是圆的直径,
是圆的直径,![]() 垂直圆所在的平面,
垂直圆所在的平面,![]() 是圆上的一点.
是圆上的一点.

(1)求证:平面 ![]() 平面
平面![]() ;
;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)先证![]() ,
,![]() ,从而
,从而![]() 平面
平面![]() ,再由面面垂直的判定定理得到平面
,再由面面垂直的判定定理得到平面![]() 平面
平面![]() .
.
(2)作![]()
![]() 平面
平面![]() ,以点
,以点![]() 为坐标原点,分别以直线
为坐标原点,分别以直线![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,利用空间向量求出直线
轴建立空间直角坐标系,利用空间向量求出直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)由![]() 是圆的直径,得
是圆的直径,得![]() ,
,
由![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,得
,得![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() .
.
(2)如图,作![]()
![]() 平面
平面![]() ,以点
,以点![]() 为坐标原点,分别以直线
为坐标原点,分别以直线![]() ,
,![]() ,
,![]() 为
为
![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
在![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
又![]() ,
,![]() ,
,![]() ,
,![]() .
.
故![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则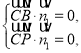
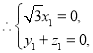 令
令![]() ,则
,则![]() .
.
![]() ,设直线
,设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
![]()
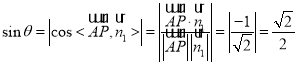 .
.
![]() 直线
直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

练习册系列答案
相关题目
【题目】设直线系M:xcosθ+(y﹣2)sinθ=1(0≤θ≤2π),对于下列四个命题:
A.M中所有直线均经过一个定点 |
B.存在定点P不在M中的任一条直线上 |
C.对于任意整数n(n≥3),存在正n边形,其所有边均在M中的直线上 |
D.M中的直线所能围成的正三角形面积都相等 |
其中真命题的代号是 (写出所有真命题的代号).