题目内容
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若![]() ,求实数
,求实数![]() 取值的集合;
取值的集合;
(Ⅱ)当![]() 时,对任意
时,对任意![]() ,
,![]() ,令
,令![]() ,证明
,证明![]() .
.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(I)f′(x)![]() .(x>0).对a分类讨论即可得出单调性极值与最值.进而得出a的取值集合;(II)当a=0时,f(x)=lnx,则
.(x>0).对a分类讨论即可得出单调性极值与最值.进而得出a的取值集合;(II)当a=0时,f(x)=lnx,则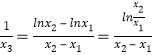 ,由(I)可知:lnx
,由(I)可知:lnx![]() 1≥0,(x>0).根据0<x1<x2,可得
1≥0,(x>0).根据0<x1<x2,可得![]() 1,ln
1,ln![]() 1
1![]() ,即可证明
,即可证明![]() .由(I)可知:lnx<x﹣1,(x>1).同理可证明:
.由(I)可知:lnx<x﹣1,(x>1).同理可证明:![]() .
.
(Ⅰ)由已知,有![]() .
.
当![]() 时,
时,![]() ,与条件
,与条件![]() 矛盾;
矛盾;
当![]() 时,若
时,若![]() ,则
,则![]() ,
,![]() 单调递减;
单调递减;
若![]() ,则
,则![]() ,
,![]() 单调递增.
单调递增.
∴![]() 在
在![]() 上有最小值
上有最小值![]() .
.
由题意![]() ,∴
,∴![]() .
.
令![]() .∴
.∴![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
∴![]() 在
在![]() 上有最大值
上有最大值![]() .∴
.∴![]() .
.
∴![]() .
.
∴![]() ,∴
,∴![]() ,
,
综上,当![]() 时,实数
时,实数![]() 取值的集合为
取值的集合为![]() .
.
(Ⅱ)当![]() 时,
时,![]() ,则
,则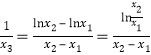 .
.
由(Ⅰ),可知![]() .
.
∴![]() (当且仅当
(当且仅当![]() 时取等号). ①
时取等号). ①
∵![]() ,∴
,∴![]() .∴
.∴![]() ,∴
,∴![]()
由①式可得当![]() 时,有
时,有![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() .
.
综上所述,有![]() ,∴
,∴![]() .
.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案【题目】某网络平台从购买该平台某课程的客户中,随机抽取了100位客户的数据,并将这100个数据按学时数,客户性别等进行统计,整理得到如表:
学时数 |
|
|
|
|
|
|
|
男性 | 18 | 12 | 9 | 9 | 6 | 4 | 2 |
女性 | 2 | 4 | 8 | 2 | 7 | 13 | 4 |
(1)根据上表估计男性客户购买该课程学时数的平均值(同一组中的数据用该组区间的中点值作代表,结果保留小数点后两位);
(2)从这100位客户中,对购买该课程学时数在20以下的女性客户按照分层抽样的方式随机抽取7人,再从这7人中随机抽取2人,求这2人购买的学时数都不低于15的概率.
(3)将购买该课程达到25学时及以上者视为“十分爱好该课程者”,25学时以下者视,为“非十分爱好该课程者”.请根据已知条件完成以下![]() 列联表,并判断是否有99.9%的把握认为“十分爱好该课程者”与性别有关?
列联表,并判断是否有99.9%的把握认为“十分爱好该课程者”与性别有关?
非十分爱好该课程者 | 十分爱好该课程者 | 合计 | |
男性 | |||
女性 | |||
合计 | 100 |
附:![]() ,
,![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |