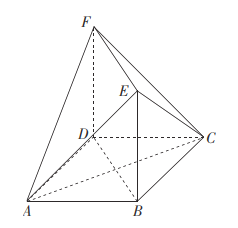
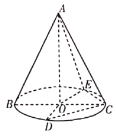
题目内容
【题目】已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求函数![]() 的解析式,并证明:
的解析式,并证明:![]() .
.
(2)已知![]() ,且函数
,且函数![]() 与函数
与函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,且线段
两点,且线段![]() 的中点为
的中点为![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() ,证明见解析; (2)证明见解析.
,证明见解析; (2)证明见解析.
【解析】
(1)利用切线方程可求得![]() 的解析式,令
的解析式,令![]() ,利用导数可求得
,利用导数可求得![]() ,从而证得结论;(2)通过分析法可知要证
,从而证得结论;(2)通过分析法可知要证![]() 成立只需证
成立只需证![]() ;令
;令![]() ,即证:
,即证:![]() ;令
;令![]() ,利用导数研究
,利用导数研究![]() 单调性,可知
单调性,可知![]() ,得到
,得到![]() 成立;令
成立;令![]() ,利用导数研究
,利用导数研究![]() 单调性,可知
单调性,可知![]() ,得到
,得到![]() 成立,可知需证的不等式成立,则原不等式成立.
成立,可知需证的不等式成立,则原不等式成立.
(1)由题意得:![]() ,即
,即![]()
又![]() ,即
,即![]() ,则
,则![]() ,解得:
,解得:![]()
则![]() .
.
令![]() ,
,![]()
令![]() ,解得:
,解得:![]()
则函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
![]() ,则:
,则:![]()
(2)要证![]() 成立,只需证:
成立,只需证:![]()
即证![]() ,即:
,即:![]()
只需证:![]()
设![]() ,即证:
,即证:![]()
要证![]() ,只需证:
,只需证:![]()
令![]() ,则
,则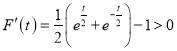
![]() 在
在![]() 上为增函数
上为增函数
![]() ,即
,即![]() 成立;
成立;
要证![]() ,只需证明:
,只需证明:![]()
令![]() ,则
,则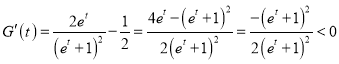
![]() 在
在![]() 上为减函数
上为减函数 ![]() ,即
,即![]() 成立
成立
![]() ,
,![]() 成立
成立
![]() 成立
成立

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
【题目】某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,统计结果如下表所示,已知这100位顾客中一次购物量超过7件的顾客占![]() .
.
一次购物量 | 1至3件 | 4至7件 | 8至11件 | 12至15件 | 16件及以上 |
顾客数(人) |
| 27 | 20 |
| 10 |
结算时间( | 0.5 | 1 | 1.5 | 2 | 2.5 |
(1)确定![]() ,
,![]() 的值,并求顾客一次购物的结算时间的平均值;
的值,并求顾客一次购物的结算时间的平均值;
(2)从收集的结算时间不超过![]() 的顾客中,按分层抽样的方法抽取5人,再从这5人中随机抽取2人,求至少有1人的结算时间为
的顾客中,按分层抽样的方法抽取5人,再从这5人中随机抽取2人,求至少有1人的结算时间为![]() 的概率.(注:将频率视为概率)
的概率.(注:将频率视为概率)