题目内容
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的方程为
的方程为![]() ,曲线
,曲线![]() 是以坐标原点
是以坐标原点![]() 为顶点,直线
为顶点,直线![]() 为准线的抛物线.以坐标原点
为准线的抛物线.以坐标原点![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立极坐标系.
轴非负半轴为极轴建立极坐标系.
(1)分别求出直线![]() 与曲线
与曲线![]() 的极坐标方程:
的极坐标方程:
(2)点![]() 是曲线
是曲线![]() 上位于第一象限内的一个动点,点
上位于第一象限内的一个动点,点![]() 是直线
是直线![]() 上位于第二象限内的一个动点,且
上位于第二象限内的一个动点,且![]() ,请求出
,请求出![]() 的最大值.
的最大值.
【答案】(1)![]()
![]() ,
,![]()
![]() ;(2)
;(2)![]()
【解析】
(1)由抛物线的准线方程易得抛物线方程,再用![]() ,
,![]() ,
,![]() 可将直线
可将直线![]() 与曲线
与曲线![]() 的直角坐标系方程转化为极坐标系方程;(2)直接在极坐标系下设点A、B的坐标,然后计算其比值,求出最大值即可.
的直角坐标系方程转化为极坐标系方程;(2)直接在极坐标系下设点A、B的坐标,然后计算其比值,求出最大值即可.
(1)因为![]() ,所以直线
,所以直线![]() 的极坐标系方程为
的极坐标系方程为![]() ,
,
又因为直线![]() 为抛物线
为抛物线![]() 的准线,所以抛物线开口朝右,且
的准线,所以抛物线开口朝右,且![]() ,即
,即![]()
所以曲线![]() 的平面直角坐标系方程为
的平面直角坐标系方程为![]() ,
,
因为![]() ,
,![]()
所以极坐标系方程为![]() ;
;
(2)设![]() ,则
,则![]() ,则
,则![]() ,
,![]() .
.
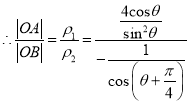
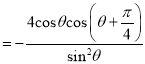
![]()
记![]() ,则
,则![]()
则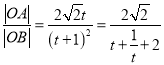
因为![]() ,当且仅当
,当且仅当![]() 时取等号
时取等号
所以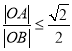
所以![]() 取最大值为
取最大值为![]() .
.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案【题目】某校针对校食堂饭菜质量开展问卷调查,提供满意与不满意两种回答,调查结果如下表(单位:人):
学生 | 高一 | 高二 | 高三 |
满意 | 500 | 600 | 800 |
不满意 | 300 | 200 | 400 |
(1)求从所有参与调查的人中任选1人是高三学生的概率;
(2)从参与调查的高三学生中,用分层抽样的方法抽取6人,在这6人中任意选取2人,求这两人对校食堂饭菜质量都满意的概率.
【题目】袋子中有四张卡片,分别写有“瓷、都、文、明”四个字,有放回地从中任取一张卡片,将三次抽取后“瓷”“都”两个字都取到记为事件![]() ,用随机模拟的方法估计事件
,用随机模拟的方法估计事件![]() 发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
发生的概率.利用电脑随机产生整数0,1,2,3四个随机数,分别代表“瓷、都、文、明”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
232 | 321 | 230 | 023 | 123 | 021 | 132 | 220 | 001 |
231 | 130 | 133 | 231 | 031 | 320 | 122 | 103 | 233 |
由此可以估计事件![]() 发生的概率为( )
发生的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【题目】高铁是一种快捷的交通工具,为我们的出行提供了极大的方便。某高铁换乘站设有编号为①,②,③,④,⑤的五个安全出口,若同时开放其中的两个安全出口,疏散![]() 名乘客所需的时间如下:
名乘客所需的时间如下:
安全出口编号 | ①② | ②③ | ③④ | ④⑤ | ①⑤ |
疏散乘客时间(s) | 120 | 220 | 160 | 140 | 200 |
则疏散乘客最快的一个安全出口的编号是( )
A. ①B. ②C. ④D. ⑤