题目内容

已知函数f（x）是单调减函数．
（1）若a＞0，比较f(a+
3
a
)与f（3）的大小；
（2）若f（|a-1|）＞f（3），求实数a的取值范围．
（1）当a＞0时，a+
3
a
≥2
a•
3
a
=2
3
＞3，
∵函数f（x）是单调减函数，
∴f(a+
3
a
)＜f（3）．
（2）∵函数f（x）是单调减函数．
∴由f（|a-1|）＞f（3），
得|a-1|＜3，
即-3＜a-1＜3，
∴-2＜a＜4，
即实数a的取值范围为-2＜a＜4，
练习册系列答案
相关题目
已知函数f（x）与g（x）的定义域均为非负实数集，对任意x≥0，规定f（x）*g（x）=minf（x），g（x），若f(x)=3-x，g(x)=
2x+5
，则f（x）*g（x）的最大值为______．
设f(x)=
sin(
π
2
x+
π
4
)		(x≤2008)
f(x-5)(x＞2008)
，则f（2007）+f（2008）+f（2009）+f（2010）=______．
设函数f（x）=（
1
4
）x-（
1
2
）x+1，不等式f（x）≤2a-1对x∈[-3，2]恒成立，则实数a的取值范围为______．
设函数f（x）是R上的减函数，若f（m-1）＞f（2m+1），则实数m的取值范围是______．
已知对数函数y=f（x）的图象过点（8，3）
（1）试求出函数f（x）的解析式．
（2）判断函数y=f（x）+3x的单调性，并说明理由．
已知函数f（x）=x2+2ax+2，x∈[-5，5]，
（1）当a=1时，求f（x）的最大值和最小值；
（2）求实数a的取值范围，使y=f（x）在区间[-5，5]上是单调函数．
已知偶函数f（x）的定义域为R，且在（-∞，0）上是增函数，M=f(
3
4
)，N=f（a2-a+1）（a∈R），则M与N的大小关系（　　）
A．M≥NB．M≤NC．M＜ND．M＞N
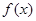已知是定义在R上的奇函数，当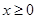时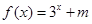（m为常数）,则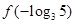的值为（ ）.
A．B．6C．4D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网