题目内容
设抛物线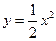
的焦点为F，准线为
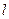，过点F作一直线与抛物线交于A、B两点，再分别过点A、B作抛物线的切线，这两条切线的交点记为P．
（1）证明：直线PA与PB相互垂直，且点P在准线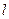上；
（2）是否存在常数
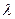，使等式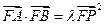
恒成立？若存在，求出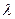的值；若不存在，说明理由．
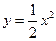的焦点为F，准线为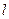，过点F作一直线与抛物线交于A、B两点，再分别过点A、B作抛物线的切线，这两条切线的交点记为P．（1）证明：直线PA与PB相互垂直，且点P在准线
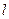上；（2）是否存在常数
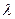，使等式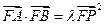恒成立？若存在，求出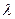的值；若不存在，说明理由．（1）证明：设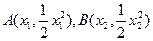
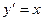
直线
直线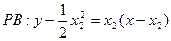
即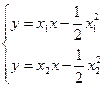
设直线AB方程：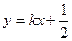
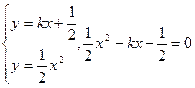
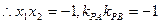
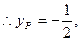
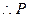在准线
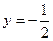上
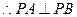
（2）存在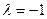
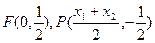
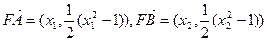
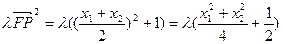
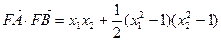
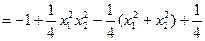
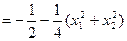
若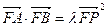
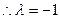
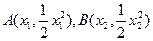
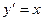
直线
直线
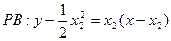
即
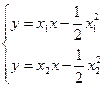
设直线AB方程：
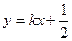
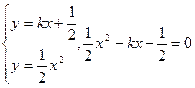
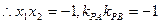
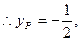
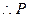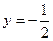在准线上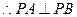（2）存在
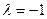
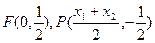
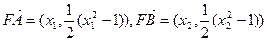
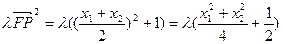
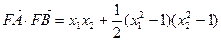
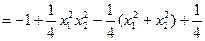
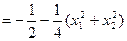
若
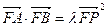
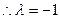
略
练习册系列答案
相关题目
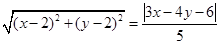表示的曲线为（ ）
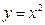上求一点P，使过点P的切线和直线3x-y+1=0的夹角为
。
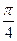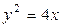上有两个定点A、B分别在对称轴的上、下两侧，F为抛物线的焦点，并且|F
A|=2，|FB|=5，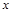
．
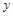满足方程
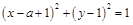，当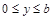
（
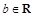）时，由此方程可以确定一个偶函数
，则抛物线
的焦点
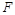到点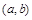
的轨迹上点的距离最大值为_________.
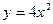在点（1,4）处的切线方程
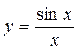在点M(π，0)处的切线的斜率
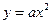(a>0)的焦点F作一直线交抛物线于P、Q两点，若线段PF与FQ的长分别为p、q，则
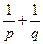等于 ( )
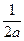C
D
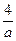
分抛物线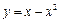
与x轴所围图形为面积相等的两部分，求k的值．