题目内容
( (本小题满分12分)
抛物线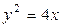 上有两个定点A、B分别在对称轴的上、下两侧,F为抛物线的焦点,并且|F
上有两个定点A、B分别在对称轴的上、下两侧,F为抛物线的焦点,并且|F A|=2,|FB|=5,
A|=2,|FB|=5,
(1)求直线AB的方程.
(2)在抛物线AOB这段曲线上求一点P,使△PAB的面积最大,并求这个最大面积.
抛物线
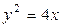 上有两个定点A、B分别在对称轴的上、下两侧,F为抛物线的焦点,并且|F
上有两个定点A、B分别在对称轴的上、下两侧,F为抛物线的焦点,并且|F A|=2,|FB|=5,
A|=2,|FB|=5,(1)求直线AB的方程.
(2)在抛物线AOB这段曲线上求一点P,使△PAB的面积最大,并求这个最大面积.
解:由已知得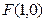 ,
, 点A在x轴上方,设A
点A在x轴上方,设A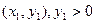 ,
,
由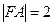 得
得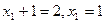 ,所以A(1,2),……2分;同理B(4,-4), …3分
,所以A(1,2),……2分;同理B(4,-4), …3分
所以直线AB的方程为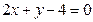 .……………………………………………4分
.……………………………………………4分
设在抛物线AOB这段曲线上任一点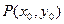 ,且
,且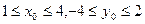 .
.
则点P到直线AB的距离d=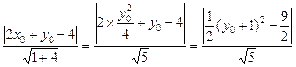 …6分
…6分
所以当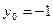 时,d取最大值
时,d取最大值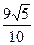 ,………7分;又
,………7分;又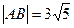 ……………8分
……………8分
所以△PAB的面积最大值为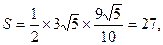 ………………………9分
………………………9分
 此
此 时P点坐标为
时P点坐标为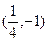
 ,
, 点A在x轴上方,设A
点A在x轴上方,设A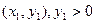 ,
,由
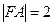 得
得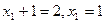 ,所以A(1,2),……2分;同理B(4,-4), …3分
,所以A(1,2),……2分;同理B(4,-4), …3分所以直线AB的方程为
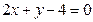 .……………………………………………4分
.……………………………………………4分设在抛物线AOB这段曲线上任一点
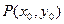 ,且
,且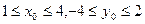 .
.则点P到直线AB的距离d=
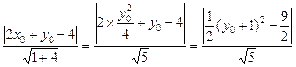 …6分
…6分所以当
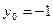 时,d取最大值
时,d取最大值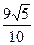 ,………7分;又
,………7分;又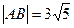 ……………8分
……………8分所以△PAB的面积最大值为
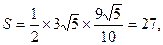 ………………………9分
………………………9分 此
此 时P点坐标为
时P点坐标为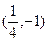
略

练习册系列答案
 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
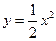 的焦点为F,准线为
的焦点为F,准线为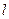 ,过点F作一直线与抛物线交于A、B两点,再分别过点A、B作抛物线的切线,这两条切线的交点记为P.
,过点F作一直线与抛物线交于A、B两点,再分别过点A、B作抛物线的切线,这两条切线的交点记为P.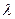 ,使等式
,使等式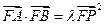 恒成立?若存在,求出
恒成立?若存在,求出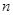 ,设抛物线
,设抛物线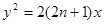 ,过
,过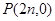 任作直线
任作直线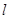 交抛物线于
交抛物线于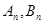 两点,则数列
两点,则数列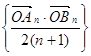 的前
的前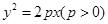 ,过点
,过点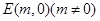 的直线交抛物线于点M、N,交y轴于点P,若
的直线交抛物线于点M、N,交y轴于点P,若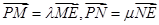 ,则
,则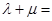 ( )
( )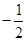
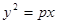 的焦点与椭圆
的焦点与椭圆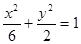 的右焦点重合,则p的值为
的右焦点重合,则p的值为

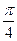
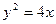 的焦点,且以
的焦点,且以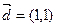 为方向向量的直线的方程是 .
为方向向量的直线的方程是 .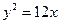 上与焦点的距离等于9的点的坐标是___________.
上与焦点的距离等于9的点的坐标是___________.