题目内容
数列{an}的前n项的和Sn=2an-1(n∈N*),数列{bn}满足:b1=3,Sn+1=an+bn(n∈N*).
(1)求证:数列{an}为等比数列;
(2)求数列{bn}的前n项的和Tn.
(1)求证:数列{an}为等比数列;
(2)求数列{bn}的前n项的和Tn.
(1)∵an+1=Sn+1-Sn=(2an+1-1)-(2an-1),
∴an+1=2an,
又a1=S1=2a1-1,∴a1=1≠0,
因此数列{an}为公比是2、首项是1的等比数列;
(2)易得bn+1-bn=2n-1,∴bn-bn-1=2n-2,bn-1-bn-2=2n-3,…,b2-b1=20=1,
以上各式相加得,bn+1-b1=1+2+3+…+2n-1=2n-1,
∴bn+1=2n+2,∴bn=2n-1+2,
∴Tn=b1+b2+…+bn=2n+
=2n+2n-1(n∈N*).
∴an+1=2an,
又a1=S1=2a1-1,∴a1=1≠0,
因此数列{an}为公比是2、首项是1的等比数列;
(2)易得bn+1-bn=2n-1,∴bn-bn-1=2n-2,bn-1-bn-2=2n-3,…,b2-b1=20=1,
以上各式相加得,bn+1-b1=1+2+3+…+2n-1=2n-1,
∴bn+1=2n+2,∴bn=2n-1+2,
∴Tn=b1+b2+…+bn=2n+
| 1-2n |
| 1-2 |

练习册系列答案
相关题目
 的前
的前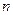 项和.
项和. +
+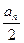 (n∈N+),则其{an}的前10项和为
(n∈N+),则其{an}的前10项和为