题目内容
在等差数列{an}中,a1=2,a1+a2+a3=12.
(1)求数列{an}的通项公式;
(2)令bn=an•3n,求数列{bn}的前n项和Sn.
(1)求数列{an}的通项公式;
(2)令bn=an•3n,求数列{bn}的前n项和Sn.
(1)∵a1=2,a1+a2+a3=3a2=12.
∴a2=4,d=a2-a1=2
∴an=2+2(n-1)=2n
(2)∵bn=an•3n=2n•3n
∴Sn=2•3+4•32+…+2n•3n
∴3Sn=2•32+4•33+…+(2n-2)•3n+2n•3n+1
两式相减可得,-2Sn=2(3+32+33+…+3n)-2n•3n+1-2n•3n+1=2×
-2n•3n+1
∴Sn=
+
•3n+1
∴a2=4,d=a2-a1=2
∴an=2+2(n-1)=2n
(2)∵bn=an•3n=2n•3n
∴Sn=2•3+4•32+…+2n•3n
∴3Sn=2•32+4•33+…+(2n-2)•3n+2n•3n+1
两式相减可得,-2Sn=2(3+32+33+…+3n)-2n•3n+1-2n•3n+1=2×
| 3(1-3n) |
| 1-3 |
∴Sn=
| 3 |
| 2 |
| (2n-1) |
| 2 |

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 :1,2,1,2,2,1,2,2,2,1,2,2,2,2,1,2,…,则数列
:1,2,1,2,2,1,2,2,2,1,2,2,2,2,1,2,…,则数列 且
且 ,则
,则 ( )
( )

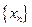 满足
满足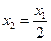 ,
,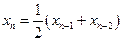 ,
,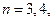 ….若
….若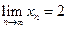 ,则( )
,则( )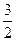 B3 C4 D5
B3 C4 D5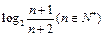 ,前n项和为Sn,则使Sn<-5成立的自然数n有
,前n项和为Sn,则使Sn<-5成立的自然数n有