题目内容
9.已知a,b(a≠b)都是正有理数,$\sqrt{a},\sqrt{b}$都是无理数.(1)判断$\sqrt{a}•\sqrt{b}$是否可能是有理数,请举例说明;
(2)求证:$\sqrt{a}+\sqrt{b}$不可能是有理数.
分析 (1)例如a=2,b=8,都是正有理数,$\sqrt{2},\sqrt{8}=2\sqrt{2}$都是无理数,而$\sqrt{a}•\sqrt{b}=\sqrt{2}•2\sqrt{2}=4$是有理数;
(2)利用反证法,即可证明.
解答 解:(1)$\sqrt{a}•\sqrt{b}$是否可能是有理数,例如a=2,b=8,都是正有理数,$\sqrt{2},\sqrt{8}=2\sqrt{2}$都是无理数,
而$\sqrt{a}•\sqrt{b}=\sqrt{2}•2\sqrt{2}=4$是有理数
(2)假设$\sqrt{a}+\sqrt{b}$是有理数,设$\sqrt{a}+\sqrt{b}=x$,
则$\sqrt{a}=x-\sqrt{b}$,两边平方得$a={x^2}-2\sqrt{b}x+b$
∴$\sqrt{b}=\frac{{{x^2}-a+b}}{2x}$,
上式左边是无理数,右边是有理数,矛盾.
∴$\sqrt{a}+\sqrt{b}$不可能是有理数.
点评 此题主要考查了反证法,正确利用反证法的一般步骤求出是解题关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
19.来晋江旅游的外地游客中,若甲、乙、丙三人选择去五店市游览的概率均为$\frac{3}{5}$,且他们的选择互不影响,则这三人中至多有两人选择去五店市游览的概率为( )
| A. | $\frac{36}{125}$ | B. | $\frac{44}{125}$ | C. | $\frac{54}{125}$ | D. | $\frac{98}{125}$ |
17.下列说法不正确的是( )
| A. | 若“p且q”为假,则p,q至少有一个是假命题 | |
| B. | 命题“?x∈R,x2-x-1<0”的否定是““?x∈R,x2-x-1≥0” | |
| C. | 当a<0时,幂函数y=xa在(0,+∞)上单调递减 | |
| D. | “φ=$\frac{π}{2}$”是“y=sin(2x+φ)为偶函数”的充要条件 |
14.已知函数f(x)=|sinx|,下列结论中错误的是( )
| A. | f(x)既偶函数,又是周期函数. | B. | f(x)的最大值为$\frac{\sqrt{3}}{2}$ | ||
| C. | y=f(x)的图象关于直线x=$\frac{π}{2}$对称 | D. | y=f(x)的图象关于直线x=π对称 |
19.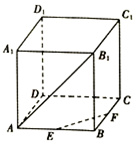 如图,在正方体ABCD-A1B1C1D1中,E、F分别为AB、BC中点,则异面直线EF与AB1所成角为( )
如图,在正方体ABCD-A1B1C1D1中,E、F分别为AB、BC中点,则异面直线EF与AB1所成角为( )
 如图,在正方体ABCD-A1B1C1D1中,E、F分别为AB、BC中点,则异面直线EF与AB1所成角为( )
如图,在正方体ABCD-A1B1C1D1中,E、F分别为AB、BC中点,则异面直线EF与AB1所成角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
 在三棱锥PABC中,G为△ABC的重心,设$\overrightarrow{PA}$=a,$\overrightarrow{PB}$=b,$\overrightarrow{PC}$=c,则$\overrightarrow{PG}$=$\frac{1}{3}$($\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}$)(用a,b,c表示).
在三棱锥PABC中,G为△ABC的重心,设$\overrightarrow{PA}$=a,$\overrightarrow{PB}$=b,$\overrightarrow{PC}$=c,则$\overrightarrow{PG}$=$\frac{1}{3}$($\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}$)(用a,b,c表示).