题目内容
10.计算:(1)${({2\frac{7}{9}})^{0.5}}+{0.1^{-2}}+{({2\frac{10}{27}})^{-\frac{2}{3}}}-3{π^0}+\frac{37}{48}$;
(2)$\frac{{lg\sqrt{27}+lg8-3lg\sqrt{10}}}{lg1.2}$.
分析 (1)首先把代分数化为假分数,然后再化简求值即可得答案.
(2)化根式为分数指数幂,然后再根据对数的运算性质化简即可得答案.
解答 解:(1)${({2\frac{7}{9}})^{0.5}}+{0.1^{-2}}+{({2\frac{10}{27}})^{-\frac{2}{3}}}-3{π^0}+\frac{37}{48}$
=$(\frac{25}{9})^{\frac{1}{2}}+1{0}^{2}+(\frac{64}{27})^{-\frac{2}{3}}-3+\frac{37}{48}$
=$\frac{5}{3}+100+\frac{9}{16}-3+\frac{37}{48}$=100;
(2)$\frac{{lg\sqrt{27}+lg8-3lg\sqrt{10}}}{lg1.2}$=$\frac{lg({3}^{3})^{\frac{1}{2}}+lg{2}^{3}-3lg1{0}^{\frac{1}{2}}}{lg\frac{3×{2}^{2}}{10}}$
=$\frac{\frac{3}{2}lg3+3lg2-\frac{3}{2}lg10}{lg3+2lg2-1}=\frac{\frac{3}{2}(lg3+2lg2-1)}{lg3+2lg2-1}$=$\frac{3}{2}$.
点评 本题考查了有理数指数幂的化简求值,考查了对数的运算性质,是基础题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
2.设函数$f(x)=\left\{\begin{array}{l}{log_2}x,x>0\\{4^{-x}}+1,x≤0\end{array}\right.$,则f(2)+f(-log23)的值为( )
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
19.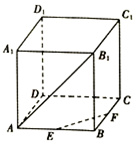 如图,在正方体ABCD-A1B1C1D1中,E、F分别为AB、BC中点,则异面直线EF与AB1所成角为( )
如图,在正方体ABCD-A1B1C1D1中,E、F分别为AB、BC中点,则异面直线EF与AB1所成角为( )
 如图,在正方体ABCD-A1B1C1D1中,E、F分别为AB、BC中点,则异面直线EF与AB1所成角为( )
如图,在正方体ABCD-A1B1C1D1中,E、F分别为AB、BC中点,则异面直线EF与AB1所成角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
1.sin300°的值为( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |