题目内容
7.若向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a}|=4,|{\overrightarrow b}|=6$,则|$\overrightarrow{a}$+$\overrightarrow{b}$|的取值范围是[2,10].分析 由题意可得-24≤$\overrightarrow{a}•\overrightarrow{b}$≤24,再根据|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{{(\overrightarrow{a}+\overrightarrow{b})}^{2}}$=$\sqrt{52+2\overrightarrow{a}•\overrightarrow{b}}$,求得|$\overrightarrow{a}$+$\overrightarrow{b}$|的取值范围.
解答 解:由$|{\overrightarrow a}|=4,|{\overrightarrow b}|=6$,可得-24≤$\overrightarrow{a}•\overrightarrow{b}$≤24,
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{{(\overrightarrow{a}+\overrightarrow{b})}^{2}}$=$\sqrt{{\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}{+\overrightarrow{b}}^{2}}$=$\sqrt{52+2\overrightarrow{a}•\overrightarrow{b}}$,
再根据 4≤52+2$\overrightarrow{a}•\overrightarrow{b}$≤100,可得$\sqrt{52+2\overrightarrow{a}•\overrightarrow{b}}$∈[2,10],
故答案为:[2,10].
点评 本题主要考查两个向量的数量积的定义,求向量的模的方法,属于基础题.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案| A. | 若“p且q”为假,则p,q至少有一个是假命题 | |
| B. | 命题“?x∈R,x2-x-1<0”的否定是““?x∈R,x2-x-1≥0” | |
| C. | 当a<0时,幂函数y=xa在(0,+∞)上单调递减 | |
| D. | “φ=$\frac{π}{2}$”是“y=sin(2x+φ)为偶函数”的充要条件 |
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
| A. | 5,10,15,20,25,30 | B. | 3,13,23,33,43,53 | ||
| C. | 1,2,3,4,5,6 | D. | 2,4,8,16,32,48 |
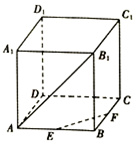 如图,在正方体ABCD-A1B1C1D1中,E、F分别为AB、BC中点,则异面直线EF与AB1所成角为( )
如图,在正方体ABCD-A1B1C1D1中,E、F分别为AB、BC中点,则异面直线EF与AB1所成角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
| A. | -2+3i | B. | 2-3i | C. | -2-3i | D. | -3i |