题目内容
设F(1,0),M点在x轴上,P点在y轴上,且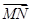 =2
=2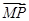 ,
,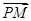 ⊥
⊥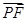 ,当点P在y轴上运动时,点N的轨迹方程为( )
,当点P在y轴上运动时,点N的轨迹方程为( )
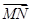 =2
=2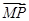 ,
,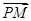 ⊥
⊥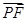 ,当点P在y轴上运动时,点N的轨迹方程为( )
,当点P在y轴上运动时,点N的轨迹方程为( )| A.y2=2x | B.y2=4x |
C.y2=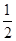 x x | D.y2=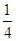 x x |
B
设M(x0,0),P(0,y0),N(x,y),
∵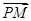 ⊥
⊥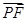 ,
,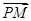 =(x0,-y0),
=(x0,-y0),
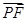 =(1,-y0),
=(1,-y0),
∴(x0,-y0)·(1,-y0)=0,
∴x0+y02=0.
由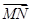 =2
=2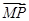 ,得(x-x0,y)=2(-x0,y0),
,得(x-x0,y)=2(-x0,y0),
∴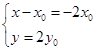 即
即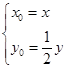
∴-x+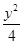 =0,
=0,
即y2=4x.
故所求的点N的轨迹方程是y2=4x.
故选B.
∵
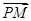 ⊥
⊥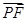 ,
,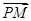 =(x0,-y0),
=(x0,-y0),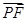 =(1,-y0),
=(1,-y0),∴(x0,-y0)·(1,-y0)=0,
∴x0+y02=0.
由
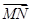 =2
=2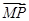 ,得(x-x0,y)=2(-x0,y0),
,得(x-x0,y)=2(-x0,y0),∴
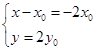 即
即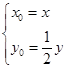
∴-x+
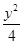 =0,
=0,即y2=4x.
故所求的点N的轨迹方程是y2=4x.
故选B.

练习册系列答案
相关题目
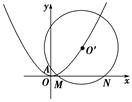
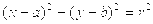 的圆心为抛物线
的圆心为抛物线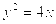 的焦点,直线3x+4y+2=0与圆C相切,则该圆的方程为( ).
的焦点,直线3x+4y+2=0与圆C相切,则该圆的方程为( ).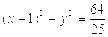
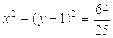
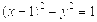
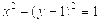
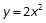 的焦点坐标是( ) .
的焦点坐标是( ) .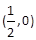
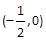
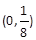
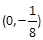
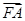 +
+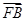 +
+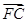 =0,则|
=0,则|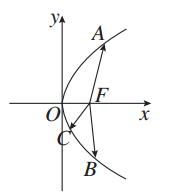
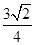 ,则点A的坐标为( )
,则点A的坐标为( )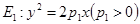 和
和 ,过原点
,过原点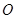 的两条直线
的两条直线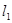 和
和 ,
, 分别交于
分别交于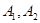 两点,
两点,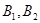 两点.
两点.
 (异于
(异于 两点.记
两点.记 与
与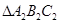 的面积分别为
的面积分别为 与
与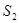 ,求
,求 的值.
的值.
 ,求曲线上距点A最近的点P的坐标及相应的距离|PA|.
,求曲线上距点A最近的点P的坐标及相应的距离|PA|.