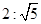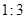题目内容
在直角坐标平面上给定一曲线y2=2x,
(1)设点A的坐标为 ,求曲线上距点A最近的点P的坐标及相应的距离|PA|.
,求曲线上距点A最近的点P的坐标及相应的距离|PA|.
(2)设点A的坐标为(a,0),a∈R,求曲线上的点到点A距离的最小值dmin,并写出dmin=f(a)的函数表达式.
(1)设点A的坐标为
 ,求曲线上距点A最近的点P的坐标及相应的距离|PA|.
,求曲线上距点A最近的点P的坐标及相应的距离|PA|.(2)设点A的坐标为(a,0),a∈R,求曲线上的点到点A距离的最小值dmin,并写出dmin=f(a)的函数表达式.
(1)|PA|= (2)dmin=f(a)=
(2)dmin=f(a)=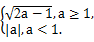
 (2)dmin=f(a)=
(2)dmin=f(a)=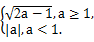
(1)设M(x,y)为曲线y2=2x上任意一点,
则|MA|2=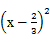 +y2=x2+
+y2=x2+ x+
x+ =
= +
+ ,
,
因为x∈[0,+∞),所以当x=0时,
|MA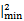 =
=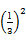 +
+ =
= ,即|MA|min=
,即|MA|min= .
.
所以距点A最近的点P坐标为(0,0),这时|PA|= .
.
(2)依题意得,
d2=(x-a)2+y2=x2-2ax+a2+2x
=x2-2(a-1)x+a2
=[x-(a-1)]2+(2a-1)
因为x∈[0,+∞),
所以分a-1≥0和a-1<0两种情况讨论.
当a≥1时,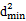 =2a-1,即dmin=
=2a-1,即dmin=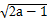 ,
,
当a<1时,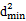 =[0-(a-1)]2+(2a-1)=a2,
=[0-(a-1)]2+(2a-1)=a2,
即dmin=|a|.
这时恰好抛物线顶点(0,0)与点A(a,0)最近.
所以dmin=f(a)=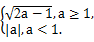
则|MA|2=
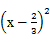 +y2=x2+
+y2=x2+ x+
x+ =
= +
+ ,
,因为x∈[0,+∞),所以当x=0时,
|MA
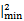 =
=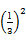 +
+ =
= ,即|MA|min=
,即|MA|min= .
.所以距点A最近的点P坐标为(0,0),这时|PA|=
 .
.(2)依题意得,
d2=(x-a)2+y2=x2-2ax+a2+2x
=x2-2(a-1)x+a2
=[x-(a-1)]2+(2a-1)
因为x∈[0,+∞),
所以分a-1≥0和a-1<0两种情况讨论.
当a≥1时,
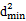 =2a-1,即dmin=
=2a-1,即dmin=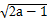 ,
,当a<1时,
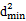 =[0-(a-1)]2+(2a-1)=a2,
=[0-(a-1)]2+(2a-1)=a2,即dmin=|a|.
这时恰好抛物线顶点(0,0)与点A(a,0)最近.
所以dmin=f(a)=

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
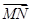 =2
=2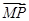 ,
,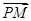 ⊥
⊥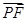 ,当点P在y轴上运动时,点N的轨迹方程为( )
,当点P在y轴上运动时,点N的轨迹方程为( )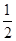 x
x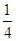 x
x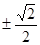
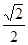
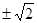
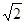
 上有一点
上有一点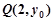 到焦点
到焦点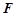 的距离为
的距离为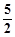 .
.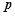 及
及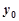 的值.
的值.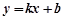 与抛物线交于两点
与抛物线交于两点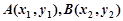 ,且
,且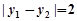 ,过弦
,过弦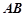 的中点
的中点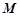 作垂直于
作垂直于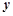 轴的直线与抛物线交于点
轴的直线与抛物线交于点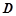 ,连接
,连接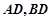 .试判断
.试判断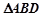 的面积是否为定值?若是,求出定值;否则,请说明理由.
的面积是否为定值?若是,求出定值;否则,请说明理由. 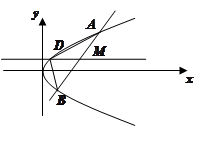
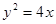 的顶点作射线
的顶点作射线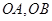 与抛物线交于
与抛物线交于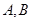 ,若
,若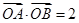 ,求证:直线
,求证:直线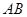 过定点.
过定点.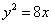 上到其焦点
上到其焦点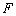 距离为5的点有( )
距离为5的点有( )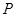 是抛物线
是抛物线 上一动点,则点
上一动点,则点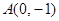 的距离与
的距离与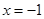 的距离和的最小值是 .
的距离和的最小值是 .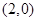 ,抛物线C:
,抛物线C: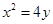 的焦点F。射线FA与抛物线C相交于点M,与其准线相交于点N,则
的焦点F。射线FA与抛物线C相交于点M,与其准线相交于点N,则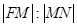 =( )
=( )