题目内容
等差数列{an}的奇数项的和为216,偶数项的和为192,首项为1,项数为奇数,求此数列的末项和通项公式.
a17=47,an=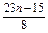 (n∈N*,n≤17).
(n∈N*,n≤17).
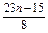 (n∈N*,n≤17).
(n∈N*,n≤17).设等差数列{an}的项数为2m+1,公差为d,
则数列的中间项为am+1,奇数项有m+1项,偶数项有m项.
依题意,有
S奇=(m+1)am+1="216 " ①
S偶=mam+1="192 " ②
①÷②,得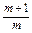 =
=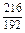 ,解得,m=8,
,解得,m=8,
∴数列共有2m+1=17项,把m=8代入②,得a9=24,
又∵a1+a17=2a9,
∴a17=2a9-a1=47,且d=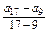 =
=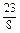 .
.
an=1+(n-1)×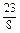 =
=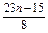 (n∈N*,n≤17).
(n∈N*,n≤17).
则数列的中间项为am+1,奇数项有m+1项,偶数项有m项.
依题意,有
S奇=(m+1)am+1="216 " ①
S偶=mam+1="192 " ②
①÷②,得
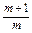 =
=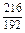 ,解得,m=8,
,解得,m=8,∴数列共有2m+1=17项,把m=8代入②,得a9=24,
又∵a1+a17=2a9,
∴a17=2a9-a1=47,且d=
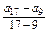 =
=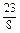 .
.an=1+(n-1)×
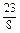 =
=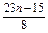 (n∈N*,n≤17).
(n∈N*,n≤17).
练习册系列答案
相关题目
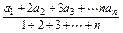 ,若{bn}为等差数列,求证:{an}也为等差数列.
,若{bn}为等差数列,求证:{an}也为等差数列.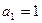 ,当
,当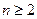 时,其前
时,其前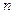 项和
项和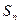 满足
满足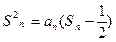
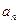 ;
;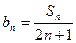 ,求数列{
,求数列{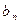 }的前项和
}的前项和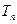
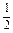 an-30,求数列{bn}的前n项和的最小值.
an-30,求数列{bn}的前n项和的最小值.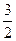 n2+
n2+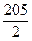 n,求数列{an}的通项公式.
n,求数列{an}的通项公式.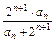 ,a1=2,求数列{an}的通项公式.
,a1=2,求数列{an}的通项公式.
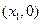 ,M
,M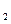
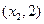 ,…,M
,…,M
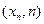 ,…,且
,…,且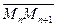 与
与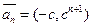
 垂直,其中是不等于零的实常数,是正整数,设
垂直,其中是不等于零的实常数,是正整数,设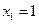 ,求数列
,求数列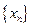 的通项公式,并求其前n项和S
的通项公式,并求其前n项和S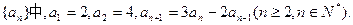 。
。 是等比数列,并求出数列
是等比数列,并求出数列 的通项公式;
的通项公式; ,数列
,数列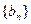 的前n项和为
的前n项和为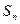 ,求使
,求使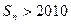 的n的最小值。
的n的最小值。