题目内容
13.已知抛物线y2=4x过焦点F的弦AB,过弦AB的中点作准线l的垂线,垂足为M,则$\overrightarrow{MA}$•$\overrightarrow{MB}$的值为0.分析 分A、B所在直线与x轴垂直与不垂直两种情况讨论,利用向量数量积运算及韦达定理计算即得结论.
解答 解:由题可知:F(1,0),准线l:x=-1.
①当A、B所在直线与x轴垂直时,易知A(1,2),B(1,-2),M(-1,0),
∴$\overrightarrow{MA}$•$\overrightarrow{MB}$=(2,2)•(2,-2)=0;
②当A、B所在直线不与x轴垂直时,设其方程为:y=k(x-1),
联立$\left\{\begin{array}{l}{y=k(x-1)}\\{{y}^{2}=4x}\end{array}\right.$,消去y可得:k2x2-(4+2k2)x+k2=0,
记A(x1,y1),B(x2,y2),
由韦达定理可知:x1+x2=$\frac{4+2{k}^{2}}{{k}^{2}}$,x1x2=1,
∴弦AB中点坐标为D($\frac{2+{k}^{2}}{{k}^{2}}$,$\frac{2}{k}$),
∴M(-1,$\frac{2}{k}$),
∴$\overrightarrow{MA}$•$\overrightarrow{MB}$=(x1+1,${y}_{1}-\frac{2}{k}$)•(x2+1,y2-$\frac{2}{k}$)
=x1x2+(x1+x2)+1+y1y2-$\frac{2}{k}$(y1+y2)+$\frac{4}{{k}^{2}}$
=x1x2+(x1+x2)+1+k2(x1-1)(x2-1)-$\frac{2}{k}$•k(x1+x2-2)+$\frac{4}{{k}^{2}}$
=(1+k2)x1x2+(-1-k2)(x1+x2)+5+k2+$\frac{4}{{k}^{2}}$
=(1+k2)+(-1-k2)$\frac{4+2{k}^{2}}{{k}^{2}}$+5+k2+$\frac{4}{{k}^{2}}$
=(1+k2)+(-1-k2)($\frac{4}{{k}^{2}}$+2)+5+k2+$\frac{4}{{k}^{2}}$
=0;
综上所述,$\overrightarrow{MA}$•$\overrightarrow{MB}$=0,
故答案为:0.
点评 本题考查抛物线的简单性质,考查运算求解能力,考查分类讨论的思想,注意解题方法的积累,属于中档题.

| A. | (-1,16) | B. | [-1,16] | C. | (-1,$\frac{13}{4}$) | D. | [-1,$\frac{13}{4}$) |
| A. | 1<e<$\sqrt{2}$ | B. | 1<e≤$\sqrt{2}$ | C. | e>$\sqrt{2}$ | D. | e≥$\sqrt{2}$ |
| A. | $\frac{8}{9}$ | B. | $\frac{1}{9}$ | C. | $-\frac{8}{9}$ | D. | $\frac{4}{9}$ |

 已知椭圆C的中心在原点O,焦点在x轴上,离心率为$\frac{1}{2}$,右焦点到右顶点的距离为1
已知椭圆C的中心在原点O,焦点在x轴上,离心率为$\frac{1}{2}$,右焦点到右顶点的距离为1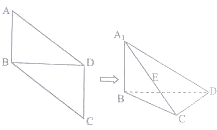 如图,在平行四边形ABCD中,AB=1,BD=$\sqrt{2}$,∠ABD=90°,将△ABD沿对角线BD折起,折后的点A变为A1,且A1C=2.
如图,在平行四边形ABCD中,AB=1,BD=$\sqrt{2}$,∠ABD=90°,将△ABD沿对角线BD折起,折后的点A变为A1,且A1C=2.