题目内容
【题目】已知F1(﹣c,0),F2(c,0)分別为双曲线![]() 1(a>0,b>0)的左、右焦点,以坐标原点O为圆心,c为半径的圆与双曲线在第二象限交于点P,若tan∠PF1F2
1(a>0,b>0)的左、右焦点,以坐标原点O为圆心,c为半径的圆与双曲线在第二象限交于点P,若tan∠PF1F2![]() ,则该双曲线的离心率为_____.
,则该双曲线的离心率为_____.
【答案】![]()
【解析】
设|PF1|=t,利用P,F1,F2在圆x2+y2=c2上,得出PF1⊥PF2,然后根据勾股定理和双曲线的定义,把![]() ,
,![]() 的值均用
的值均用![]() 来表示,进而可以求得该双曲线的离心率
来表示,进而可以求得该双曲线的离心率
由题意可得:P,F1,F2在圆x2+y2=c2上,所以PF1⊥PF2,设|PF1|=t,因为tan∠PF1F2![]() ,
,
所以|PF2|![]() ,由勾股定理可得t2+2t2=4c2,所以4c2=3t2,所以2c
,由勾股定理可得t2+2t2=4c2,所以4c2=3t2,所以2c![]() t,
t,
而2a=|PF2|﹣|PF1|![]() (
(![]() )t,所以双曲线的离心率e
)t,所以双曲线的离心率e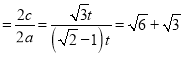 ,
,
故答案为:![]()

练习册系列答案
相关题目