题目内容
【题目】三位数中,如果百位数字、十位数字、个位数字刚好能构成等差数列,则称为“等差三位数”,例如:147,642,777,420等等.等差三位数的总个数为( )
A.32B.36C.40D.45
【答案】D
【解析】
由题意分公差为0,1,2,3,4,-1,-2,-3,-4九种情况,分别得出各三位数的个数,运用加法原理可得选项.
由题意得若百位数字、十位数字、个位数字构成公差为0的“等差三位数”,则只要各位数字不为零即可,有9个;
若百位数字、十位数字个位数字构成公差为1的“等差三位数”,则百位数字不大于7,有7个;
若百位数字、十位数字、个位数字构成公差为2的“等差三位数”,则百位数字不大于5,有5个;
若百位数字十位数字个位数字构成公差为3的“等差三位数”,则百位数字不大于3,有3个;若百位数字、十位数字、个位数字构成公差为4的“等差三位数”,则百位数字只能为1,有1个;
若百位数字、十位数字、个位数字构成公差为![]() 的“等差三位数,则百位数字不小于2,有8个;
的“等差三位数,则百位数字不小于2,有8个;
若百位数字、十位数字、个位数字构成公差为![]() 的“等差三位数”,则百位数字不小于4,有6个;
的“等差三位数”,则百位数字不小于4,有6个;
若百位数字、十位数字、个位数字构成公差为![]() 的“等差三位数”,则百位数字不小于6,有4个;
的“等差三位数”,则百位数字不小于6,有4个;
若百位数字、十位数字个位数字构成公差为![]() 的“等差三位数”,则百位数字不小于8有2个.
的“等差三位数”,则百位数字不小于8有2个.
综上所述,“等差三位数”的总数为![]() 个,
个,
故选:D.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案【题目】基于移动互联技术的共享单车被称为“新四大发明”之一,短时间内就风靡全国,带给人们新的出行体验,某共享单车运营公司的市场研究人员为了解公司的经营状况,对该公司最近六个月内的市场占有率进行了统计,设月份代码为x,市场占有率为y(%),得结果如下表
年月 | 2019.11 | 2019.12 | 2020.1 | 2020.2 | 2020.3 | 2020.4 |
x | 1 | 2 | 3 | 4 | 5 | 6 |
y | 9 | 11 | 14 | 13 | 18 | 19 |
(1)观察数据,可用线性回归模型拟合y与x的关系,请用相关系数加以说明(精确到0.001);
(2)求y关于x的线性回归方程,并预测该公司2020年6月份的市场占有率;
(3)根据调研数据,公司决定再采购一批单车投入市场,现有采购成本分别为1000元/辆和800元/辆的甲、乙两款车型,报废年限不相同.考虑到公司的经济效益,该公司决定先对这两款单车各100辆进行科学模拟测试,得到两款单车使用寿命统计如下表:
车辆数 车型 | 1年 | 2年 | 3年 | 4年 | 总计 |
甲款 | 10 | 40 | 30 | 20 | 100 |
乙款 | 15 | 35 | 40 | 10 | 100 |
经测算,平均每辆单车每年可以为公司带来收入500元,不考虑除采购成本之外的其他成本,假设每辆单车的使用寿命都是整数年,且用频率估计每辆单车使用寿命的概率,以每辆单车产生利润的期望值为决策依据,如果你是该公司的负责人,你会选择采购哪款车型?
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式,相关系数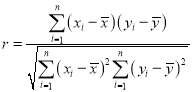 ,回归方程
,回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为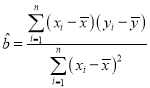 ,
,![]() .
.