题目内容
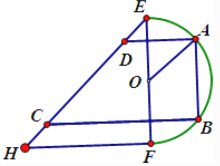
【题目】为了制作广告牌,需在如图所示的铁片上切割出一个直角梯形,已知铁片由两部分组成,半径为1的半圆![]() 及等腰直角三角形
及等腰直角三角形![]() ,其中
,其中![]() ,为裁剪出面积尽可能大的梯形铁片
,为裁剪出面积尽可能大的梯形铁片![]() (不计损耗),将点
(不计损耗),将点![]() 放在弧
放在弧![]() 上,点
上,点![]() 放在斜边
放在斜边![]() 上,且
上,且![]() ,设
,设![]() .
.
(1)求梯形铁片![]() 的面积
的面积![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)试确定![]() 的值,使得梯形铁片
的值,使得梯形铁片![]() 的面积
的面积![]() 最大,并求出最大值.
最大,并求出最大值.
【答案】(1)![]() ,其中
,其中![]() .(2)
.(2)![]() 时,
时, ![]()
【解析】试题分析:(1)求梯形铁片![]() 的面积
的面积![]() 关键是用
关键是用![]() 表示上下底及高,先由图形得
表示上下底及高,先由图形得![]() ,这样可得高
,这样可得高![]() ,再根据等腰直角三角形性质得
,再根据等腰直角三角形性质得![]() ,
, ![]() 最后根据梯形面积公式得
最后根据梯形面积公式得![]()
![]() ,交代定义域
,交代定义域![]() .(2)利用导数求函数最值:先求导数
.(2)利用导数求函数最值:先求导数![]()
![]() ,再求导函数零点
,再求导函数零点![]() ,列表分析函数单调性变化规律,确定函数最值
,列表分析函数单调性变化规律,确定函数最值
试题解析:(1)连接![]() ,根据对称性可得
,根据对称性可得![]() 且
且![]() ,
,
所以![]() ,
, ![]() ,
, ![]() ,
,
所以![]()
![]() ,其中
,其中![]() .
.
(2)记![]() ,
, ![]() ,
,
![]()
![]() (
(![]() ).
).
当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以![]() ,即
,即![]() 时,
时, ![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目