题目内容
20.函数f(x)=|x+1|+|x-1|+$\sqrt{4-{x}^{2}}$的值域[2+$\sqrt{3}$,2$\sqrt{5}$].分析 转化为y=$\left\{\begin{array}{l}{2x+\sqrt{4-{x}^{2}}1<x≤2}\\{2+\sqrt{4-{x}^{2}},-1≤x≤1}\\{-2x+\sqrt{4-{x}^{2}},-2≤x<-1}\end{array}\right.$利用奇偶性,导数判断单调性,求解最值,即可求解值域.
解答 解;∵f(-x)=|-x+1|+|-x-1|=|x-1|+|x+1|$+\sqrt{4-{x}^{2}}$=f(x)
∴f(x)是偶函数
∵函数f(x)=|x+1|+|x-1|+$\sqrt{4-{x}^{2}}$,的定义域为[-2,2],
∴y=$\left\{\begin{array}{l}2x+\sqrt{4-{x}^{2}},1<x≤2\\ 2+\sqrt{4-{x}^{2}},-1≤x≤1\\-2x+\sqrt{4-{x}^{2}},-2≤x<-1\end{array}\right.$,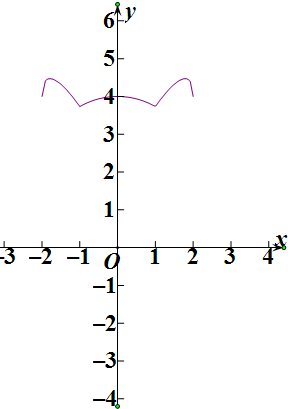
f(x)=2+$\sqrt{4-{x}^{2}}$在[-1,0]单调递增,[0,1]单调递减
最小值为f(1)=2$+\sqrt{3}$,
∵y=2x$+\sqrt{4-{x}^{2}}$,1<x≤2,
y′=2-$\frac{x}{\sqrt{4-{x}^{2}}}$,
y′=0,x2=$\frac{16}{5}$,x=$\frac{4\sqrt{5}}{5}$
∴在[1,2]上最大值f($\frac{4\sqrt{5}}{5}$)=2$\sqrt{5}$,
∴f(x)的值域为[2+$\sqrt{3}$,2$\sqrt{5}$],
故答案为:[2+$\sqrt{3}$,2$\sqrt{5}$],
点评 本题较复杂,运用分段函数表示出来之后利用单调性,结合导数判断的递增求解最大值最小值,难度较大,考查了学生解决问题的能力,思维.

| A. | 46 | B. | 44 | C. | 33 | D. | 45 |
| A. | x>-3 | B. | x<-3 | ||
| C. | x=-3 | D. | x与-3的大小不确定 |
