题目内容
15.在一个平面直角坐标系中,求下列方程所对应的图形经过伸缩变换$\left\{\begin{array}{l}{x′=\frac{1}{3}x}\\{y′=\frac{1}{2}y}\end{array}\right.$后的图形.(1)$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1
(2)$\frac{{x}^{2}}{18}$-$\frac{{y}^{2}}{12}$=1
(3)y2=2x.
分析 由伸缩变换$\left\{\begin{array}{l}{x′=\frac{1}{3}x}\\{y′=\frac{1}{2}y}\end{array}\right.$可得$\left\{\begin{array}{l}{x=3{x}^{′}}\\{y=2{y}^{′}}\end{array}\right.$.分别代入所给的曲线方程中,即可判断出曲线类型.
解答 解:由伸缩变换$\left\{\begin{array}{l}{x′=\frac{1}{3}x}\\{y′=\frac{1}{2}y}\end{array}\right.$可得$\left\{\begin{array}{l}{x=3{x}^{′}}\\{y=2{y}^{′}}\end{array}\right.$.
(1)把$\left\{\begin{array}{l}{x=3{x}^{′}}\\{y=2{y}^{′}}\end{array}\right.$代入$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1可得:(x′)2+(y′)2=1,是以原点为圆心、1为半径的圆.
(2)把$\left\{\begin{array}{l}{x=3{x}^{′}}\\{y=2{y}^{′}}\end{array}\right.$代入$\frac{{x}^{2}}{18}$-$\frac{{y}^{2}}{12}$=1,可得:$\frac{({x}^{′})^{2}}{2}-\frac{({y}^{′})^{2}}{3}=1$,仍然为以坐标轴为对称轴的双曲线.
(3)把$\left\{\begin{array}{l}{x=3{x}^{′}}\\{y=2{y}^{′}}\end{array}\right.$代入y2=2x,可得$({y}^{′})^{2}=\frac{3}{2}{x}^{′}$,仍然为以x轴为对称轴的抛物线.
点评 本题考查了圆锥曲线的伸缩变换,考查了计算能力,属于基础题.


| A. | i<99 | B. | i>99 | C. | i<100 | D. | i>100 |
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
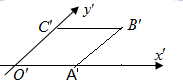 已知用斜二测画法得到四边形OABC的直观图是边长为2的菱形O′A′B′C′,如图所示,则四边形OABC的面积是( )
已知用斜二测画法得到四边形OABC的直观图是边长为2的菱形O′A′B′C′,如图所示,则四边形OABC的面积是( )