题目内容
20.已知sin(3π+α)=2cos(α-4π),求$\frac{cos(\frac{π}{2}-α)+5sin(\frac{π}{2}+α)}{2cos(π+α)-sin(-α)}$的值.分析 先化简sin(3π+α)=2cos(α-4π),再代入$\frac{cos(\frac{π}{2}-α)+5sin(\frac{π}{2}+α)}{2cos(π+α)-sin(-α)}$中求值即可.
解答 解:∵sin(3π+α)=2cos(α-4π),
∴-sinα=2cos(4π-α)=2cosα,
∴sinα=-2cosα
∴$\frac{cos(\frac{π}{2}-α)+5sin(\frac{π}{2}+α)}{2cos(π+α)-sin(-α)}$=$\frac{sinα+5cosα}{-2cosα+sinα}$
=$\frac{-2cosα+5cosα}{-2cosα-2cosα}$
=$\frac{3cosα}{-4cosα}$
=-$\frac{3}{4}$.
点评 本题考查了同角的三角函数的关系以及诱导公式的应用问题,是基础题目.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案
相关题目
10.在集合{1,2,3,4}中任取一个偶数a和一个奇数b构成以原点为起点的向量$\overrightarrow{α}$=(a,b).从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形.记所有作成的平行四边形的个数为n,其中面积不超过4的平行四边形的个数为m,则$\frac{m}{n}$=( )
| A. | $\frac{4}{15}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{2}{3}$ |
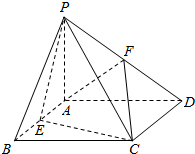 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,E、F别是AB、PD的中点.若PA=AD=CD=4.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,E、F别是AB、PD的中点.若PA=AD=CD=4.