题目内容
10.在集合{1,2,3,4}中任取一个偶数a和一个奇数b构成以原点为起点的向量$\overrightarrow{α}$=(a,b).从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形.记所有作成的平行四边形的个数为n,其中面积不超过4的平行四边形的个数为m,则$\frac{m}{n}$=( )| A. | $\frac{4}{15}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{2}{3}$ |
分析 本题是一个等可能事件的概率,a的取法有2种,b的取法有3种,故向量$\overrightarrow{a}$=(a,b)有6个,从中任取两个向量共C62=15中取法,平行四边形的面积超过4的由列举法列出,得到结果.
解答 解:由题意知本题是一个等可能事件的概率,
试验发生包含的事件是从数字中选出两个数字,组成向量,
a的取法有2种,b的取法有3种,故向量$\overrightarrow{a}$=(a,b)有6个,
从中任取两个向量共C62=15种结果,
其中面积为1的平行四边形的个数为3,即(2,3)(4,5);(2,1)(4,3);(2,1)(4,1);
其中面积为2的平行四边形的个数为2,即(2,3)(2,5);(2,1)(2,3);
其中面积为3的平行四边形的个数为2,即(2,3)(4,3);(2,1)(4,5);
其中面积为4的平行四边形的个数为3,即(2,1)(2,5);(4,1)(4,3);(4,3)(4,5);
其中面积为5的平行四边形的个数为2,即(2,3)(4,1);(2,5)(4,5);
其中面积为7的平行四边形的个数为1,即(2,5)(4,3);
其中面积为8的平行四边形的个数为1,即(4,1)(4,5);
其中面积为9的平行四边形的个数为,即(2,5)(4,1).
满足条件的事件是平行四边形的面积不超过4的由列举法列出共有10个,
根据等可能事件的概率得到P=$\frac{10}{15}$=$\frac{2}{3}$,
故选:D.
点评 本题考查等可能事件的概率,考查组合数的应用,考查用列举法列举法求计数问题,本题是一个综合题目.

练习册系列答案
相关题目
18.已知f(x)=x2+2xf′(1)-6,则f′(1)等于( )
| A. | 4 | B. | -2 | C. | 0 | D. | 2 |
5.已知复数z=$\frac{2+i}{i^3}$,z的共轭复数是$\overline{z}$,则$\overline{z}$对应的点位于复平面内的( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
2.函数$y=\frac{{{{(x-1)}^0}}}{{\sqrt{|x|+x}}}$的定义域是( )
| A. | (0,+∞) | B. | (0,1)∪(1,+∞) | C. | (-∞,0) | D. | (-∞,-1)∪(0,+∞) |
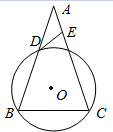 如图,圆O的半径为2,等腰△ABC的底边的两端点B,C在圆O上,AB与圆O交于点D,AD=2,圆O的切线DE交AC于E点.
如图,圆O的半径为2,等腰△ABC的底边的两端点B,C在圆O上,AB与圆O交于点D,AD=2,圆O的切线DE交AC于E点.