题目内容
12.已知命题p:?x∈R,x2+(a-1)x+1≥0成立,命题q:?x0∈R,ax${\;}_{0}^{2}$-2ax0-3>0不成立,若p假q 真.求实数a的取值范围.分析 求出命题p,q为真命题时,a的范围,据p假q真.求实数a的取值范围.
解答 解:命题p:?x∈R,x2+(a-1)x+1≥0成立,则△≤0,可得-1≤a≤3;
命题q:?x0∈R,ax${\;}_{0}^{2}$-2ax0-3>0不成立,则ax2-2ax-3≤0恒成立,∴a=0或$\left\{\begin{array}{l}{a<0}\\{4{a}^{2}+12a≤0}\end{array}\right.$,∴-3≤a≤0.
∵p假q真,
∴$\left\{\begin{array}{l}{a<-1或a>3}\\{-3≤a≤0}\end{array}\right.$,
∴-3≤a<-1.
点评 本题考查复合函数的真假与构成其简单命题的真假的关系,解决此类问题应该先求出简单命题为真时参数的范围.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
2.函数$y=\frac{{{{(x-1)}^0}}}{{\sqrt{|x|+x}}}$的定义域是( )
| A. | (0,+∞) | B. | (0,1)∪(1,+∞) | C. | (-∞,0) | D. | (-∞,-1)∪(0,+∞) |
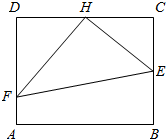 某高校专家楼前现有一块矩形草坪ABCD,已知草坪长AB=100米,宽BC=50$\sqrt{3}$米,为了便于专家平时工作、起居,该高校计划在这块草坪内铺设三条小路HE、HF和EF,并要求H是CD的中点,点E在边BC上,点F在边AD上,且∠EHF为直角,如图所示.
某高校专家楼前现有一块矩形草坪ABCD,已知草坪长AB=100米,宽BC=50$\sqrt{3}$米,为了便于专家平时工作、起居,该高校计划在这块草坪内铺设三条小路HE、HF和EF,并要求H是CD的中点,点E在边BC上,点F在边AD上,且∠EHF为直角,如图所示.