题目内容
15.设a1,a2,…a2014都是正数且a1+a2+…+a2014=1.则$\frac{{{a}_{1}}^{2}}{2+{a}_{1}}$+$\frac{{{a}_{2}}^{2}}{2+{a}_{2}}$+…$\frac{{{a}_{2013}}^{2}}{2+{a}_{2013}}$+$\frac{{{a}_{2014}}^{2}}{2+{a}_{2014}}$的最小值为$\frac{1}{4029}$.分析 利用柯西不等式的变形:设a1,a2,…an为实数,b1,b2,…bn为正数,则$\frac{{{a}_{1}}^{2}}{{b}_{1}}$+$\frac{{{a}_{2}}^{2}}{{b}_{2}}$+…+$\frac{{{a}_{n}}^{2}}{{b}_{n}}$≥$\frac{({a}_{1}+{a}_{2}+…+{a}_{n})^{2}}{{b}_{1}+{b}_{2}+…+{b}_{n}}$当且仅当$\frac{{a}_{1}}{{b}_{1}}$=$\frac{{a}_{2}}{{b}_{2}}$=…=$\frac{{a}_{n}}{{b}_{n}}$时取等号,计算即得结论.
解答 解:$\frac{{{a}_{1}}^{2}}{2+{a}_{1}}$+$\frac{{{a}_{2}}^{2}}{2+{a}_{2}}$+…$\frac{{{a}_{2013}}^{2}}{2+{a}_{2013}}$+$\frac{{{a}_{2014}}^{2}}{2+{a}_{2014}}$≥$\frac{({a}_{1}+{a}_{2}+…+{a}_{2014})^{2}}{2×2014+({a}_{1}+{a}_{2}+…+{a}_{2014})}$=$\frac{1}{4028+1}$=$\frac{1}{4029}$,
当且仅当$\frac{{a}_{1}}{2+{a}_{1}}$=$\frac{{a}_{2}}{2+{a}_{2}}$=…=$\frac{{a}_{2014}}{2+{a}_{2014}}$取等号,
故答案为:$\frac{1}{4029}$.
点评 本题考查柯西不等式的变形,注意解题方法的积累,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
5.若直线y=x+b与曲线x2-4x+y2-6y+9=0(y≤3)有公共点,则b的取值范围是( )
| A. | [-1,1+2$\sqrt{2}$] | B. | [1-2$\sqrt{2}$,1+2$\sqrt{2}$] | C. | [1-2$\sqrt{2}$,3] | D. | [1-$\sqrt{2}$,3] |
6.已知y=f(x)是定义在R上的单调函数,任意实数x1,x2满足x1<x2,λ≠-1,α=$\frac{{x}_{1}+λ{x}_{2}}{1+λ}$,β=$\frac{λ{x}_{1}+{x}_{2}}{1+λ}$,若|f(x1)-f(x2)|<|f(α)-f(β)|恒成立,则有( )
| A. | 0<λ<1 | B. | λ=0 | C. | λ<0且λ≠-1 | D. | λ≥1 |
5.已知复数z=$\frac{2+i}{i^3}$,z的共轭复数是$\overline{z}$,则$\overline{z}$对应的点位于复平面内的( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
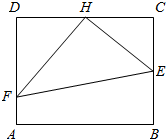 某高校专家楼前现有一块矩形草坪ABCD,已知草坪长AB=100米,宽BC=50$\sqrt{3}$米,为了便于专家平时工作、起居,该高校计划在这块草坪内铺设三条小路HE、HF和EF,并要求H是CD的中点,点E在边BC上,点F在边AD上,且∠EHF为直角,如图所示.
某高校专家楼前现有一块矩形草坪ABCD,已知草坪长AB=100米,宽BC=50$\sqrt{3}$米,为了便于专家平时工作、起居,该高校计划在这块草坪内铺设三条小路HE、HF和EF,并要求H是CD的中点,点E在边BC上,点F在边AD上,且∠EHF为直角,如图所示.