题目内容
12.若sin($\frac{π}{3}$-α)=$\frac{4}{5}$,则cos(2α+$\frac{π}{3}$)=$\frac{7}{25}$.分析 由条件利用诱导公式求得cos($\frac{π}{6}$+α)的值,再利用二倍角的余弦公式求得cos(2α+$\frac{π}{3}$)的值.
解答 解:∵sin($\frac{π}{3}$-α)=cos($\frac{π}{6}$+α)=$\frac{4}{5}$,∴cos(2α+$\frac{π}{3}$)=2${cos}^{2}(α+\frac{π}{6})$-1=2×$\frac{16}{25}$-1=$\frac{7}{25}$,
故答案为:$\frac{7}{25}$.
点评 本题主要考查诱导公式,二倍角的余弦公式的应用,属于基础题.

练习册系列答案
相关题目
2.复数i2015(i为虚数单位)的共轭复数是( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
3.在等比数列{an}中,若a3=4,a7=16,a5的值为( )
| A. | ±8 | B. | 4 | C. | 8 | D. | 64 |
17.给出下列实际问题:①一种药物对某种病的治愈率;②两种药物冶疗同一种病是否有区别;③吸烟者得肺病的概率;④吸烟人群是否与性别有关系;⑤网吧与青少年的犯罪是否有关系.其中,用独立性检验可以解决的问题有( )
| A. | ①②③ | B. | ②④⑤ | C. | ②③④⑤ | D. | ①②③④⑤ |
4.设全集U=R,集合R={0,1,2},B={x|$\frac{1}{x-1}$>0,x∈R},则A∩∁UB=( )
| A. | {0} | B. | {0,1} | C. | {1,2} | D. | {0,1,2} |
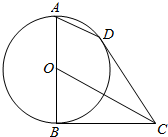 如图所示,AB为圆O的直径,BC,CD为圆O的切线,B,D为切点.
如图所示,AB为圆O的直径,BC,CD为圆O的切线,B,D为切点.