题目内容
设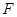 为抛物线
为抛物线 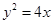 的焦点,
的焦点,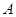 、
、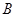 、
、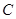 为该抛物线上三点,若
为该抛物线上三点,若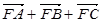 =0,则
=0,则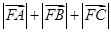 的值为
的值为
 为抛物线
为抛物线 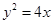 的焦点,
的焦点,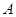 、
、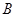 、
、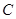 为该抛物线上三点,若
为该抛物线上三点,若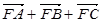 =0,则
=0,则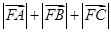 的值为
的值为| A.3 | B.4 | C.6 | D.9 |
C
分析:先设A(x1,y1),B(x2,y2),C(x3,y3),根据抛物线方程求得焦点坐标和准线方程,再依据
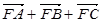 =0,判断点F是△ABC重心,进而可求x1+x2+x3的值.最后根据抛物线的定义求得答案.
=0,判断点F是△ABC重心,进而可求x1+x2+x3的值.最后根据抛物线的定义求得答案.解:设A(x1,y1),B(x2,y2),C(x3,y3)
抛物线焦点坐标F(1,0),准线方程:x=-1
∵
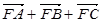 =0,
=0,∴点F是△ABC重心
则x1+x2+x3=3
y1+y2+y3=0
而|FA|=x1-(-1)=x1+1
|FB|=x2-(-1)=x2+1
|FC|=x3-(-1)=x3+1
∴|FA|+|FB|+|FC|=x1+1+x2+1+x3+1=(x1+x2+x3)+3=3+3=6
故选C

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
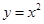 的准线方程是 ( )
的准线方程是 ( )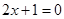
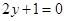
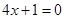
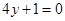
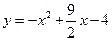 ,通过原点O作C的切线
,通过原点O作C的切线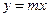 ,使切点P在第一象限.
,使切点P在第一象限. 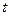 ,为使DOPQ的面积小于DPQR的面积,试求
,为使DOPQ的面积小于DPQR的面积,试求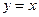 对称,则C2的准线方程是 .
对称,则C2的准线方程是 .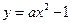 的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为 。
的焦点是坐标原点,则以抛物线与两坐标轴的三个交点为顶点的三角形面积为 。 是抛物线
是抛物线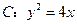 的焦点,过
的焦点,过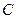 于
于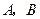 两点。设
两点。设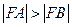 ,则
,则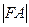 与
与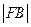 的比值等于 。
的比值等于 。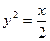 与圆
与圆 有且只有三个公共点,则a的取值范围是( )
有且只有三个公共点,则a的取值范围是( )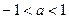
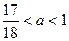
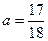

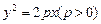 的焦点为
的焦点为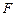 ,准线
,准线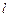 与
与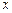 轴交于点
轴交于点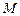 ,若
,若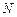 为
为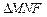 为等腰三角形,
为等腰三角形,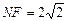 时,则
时,则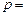 _____.
_____.