题目内容
(本题满分14分)设有抛物线C: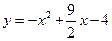 ,通过原点O作C的切线
,通过原点O作C的切线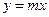 ,使切点P在第一象限.
,使切点P在第一象限.
(1)求m的值,以及P的坐标;
(2)过点P作切线的垂线,求它与抛物线的另一个交点Q;
(3)设C上有一点R,其横坐标为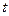 ,为使DOPQ的面积小于DPQR的面积,试求
,为使DOPQ的面积小于DPQR的面积,试求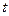 的取值范围.
的取值范围.
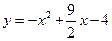 ,通过原点O作C的切线
,通过原点O作C的切线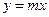 ,使切点P在第一象限.
,使切点P在第一象限. (1)求m的值,以及P的坐标;
(2)过点P作切线的垂线,求它与抛物线的另一个交点Q;
(3)设C上有一点R,其横坐标为
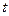 ,为使DOPQ的面积小于DPQR的面积,试求
,为使DOPQ的面积小于DPQR的面积,试求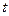 的取值范围.
的取值范围.(1)斜率k= ,P的坐标为(2,1)
,P的坐标为(2,1)
(2)Q点的坐标为( ,-4)
,-4)
(3)t的取值 范围为t<
范围为t<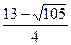 或t>
或t>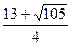 .
.
 ,P的坐标为(2,1)
,P的坐标为(2,1)(2)Q点的坐标为(
 ,-4)
,-4)(3)t的取值
 范围为t<
范围为t<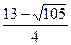 或t>
或t>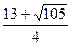 .
.设点P的坐标为(x1, y1),则y1=kx1……①,y1= –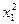 +
+ x1 – 4……②,
x1 – 4……②,
①代入②,得: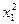 +(k–
+(k– )x1+4=0………
)x1+4=0………
 …………………………………………2分
…………………………………………2分
因为点P为切点,所以(k– )2–16=0,得:k=
)2–16=0,得:k= 或k=
或k= ……………………4分
……………………4分
当k= 时x1= -2,y1= -1
时x1= -2,y1= -1 7;当k=
7;当k= 时,x1= 2,y1= 1;
时,x1= 2,y1= 1;
因为点P在第一象限,故所求的斜率k= ,P的坐标为(2,1),……………6分
,P的坐标为(2,1),……………6分
法二:求导
(2)过 P点作切线的垂线,其方程为:y=-2x+5……③,代入抛物线方程,得:
x2-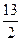 x+9=0,设Q点的坐标为(x2, y2),则2x2=9,所以x2=
x+9=0,设Q点的坐标为(x2, y2),则2x2=9,所以x2= ,y2=-4,
,y2=-4,
所以Q点的坐标为( ,-4),………………………
,-4),……………………… ………
……… ………………10分
………………10分
(3)设C上有一点R(t,-t2+ t–4),它到直线PQ的距离为:
t–4),它到直线PQ的距离为:
d=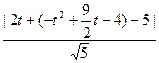 =
=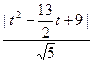 ……………………………………12分
……………………………………12分
点O到直线PQ的距离PO =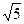 ,SDOPQ=
,SDOPQ= ´PQ´OP,SDPQR=
´PQ´OP,SDPQR= ´PQ´d,
´PQ´d,
因为DOPQ的面积小于DPQR的面积,SDOPQ < SDPQR,
 即:
即: OP < d,即:
OP < d,即: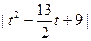 >5,……………………………………14分
>5,……………………………………14分
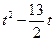 +4>0或
+4>0或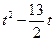 +14<0
+14<0
解之得:t<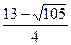 或t>
或t>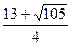
所以t的取值 范围为t<
范围为t<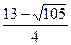 或t>
或t>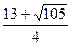 .……………………………16分
.……………………………16分
法二:做平行线
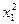 +
+ x1 – 4……②,
x1 – 4……②,①代入②,得:
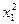 +(k–
+(k– )x1+4=0………
)x1+4=0………
 …………………………………………2分
…………………………………………2分因为点P为切点,所以(k–
 )2–16=0,得:k=
)2–16=0,得:k= 或k=
或k= ……………………4分
……………………4分当k=
 时x1= -2,y1= -1
时x1= -2,y1= -1 7;当k=
7;当k= 时,x1= 2,y1= 1;
时,x1= 2,y1= 1;因为点P在第一象限,故所求的斜率k=
 ,P的坐标为(2,1),……………6分
,P的坐标为(2,1),……………6分法二:求导
(2)过 P点作切线的垂线,其方程为:y=-2x+5……③,代入抛物线方程,得:
x2-
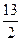 x+9=0,设Q点的坐标为(x2, y2),则2x2=9,所以x2=
x+9=0,设Q点的坐标为(x2, y2),则2x2=9,所以x2= ,y2=-4,
,y2=-4,所以Q点的坐标为(
 ,-4),………………………
,-4),……………………… ………
……… ………………10分
………………10分(3)设C上有一点R(t,-t2+
 t–4),它到直线PQ的距离为:
t–4),它到直线PQ的距离为:d=
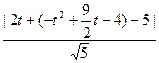 =
=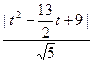 ……………………………………12分
……………………………………12分点O到直线PQ的距离PO =
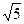 ,SDOPQ=
,SDOPQ= ´PQ´OP,SDPQR=
´PQ´OP,SDPQR= ´PQ´d,
´PQ´d,因为DOPQ的面积小于DPQR的面积,SDOPQ < SDPQR,
 即:
即: OP < d,即:
OP < d,即: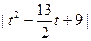 >5,……………………………………14分
>5,……………………………………14分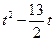 +4>0或
+4>0或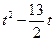 +14<0
+14<0解之得:t<
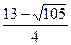 或t>
或t>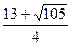
所以t的取值
 范围为t<
范围为t<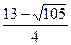 或t>
或t>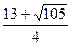 .……………………………16分
.……………………………16分法二:做平行线

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
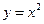 和三个点
和三个点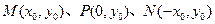
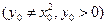 ,过点
,过点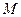 的一条直线交抛物线于
的一条直线交抛物线于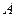 、
、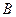 两点,
两点,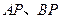 的延长线分别交曲线
的延长线分别交曲线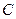 于
于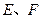 .
.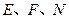 三点共线;
三点共线;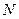 四点共线,问:是否存在
四点共线,问:是否存在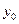 ,使以线段
,使以线段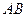 为直径的圆与抛物线有异于
为直径的圆与抛物线有异于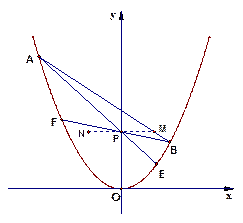
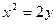
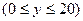 ,在杯中放入一个球,要使球触及酒杯的底部,则球的半径
,在杯中放入一个球,要使球触及酒杯的底部,则球的半径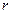 的取值范围是 。
的取值范围是 。 为抛物线
为抛物线 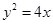 的焦点,
的焦点, 、
、 、
、 为该抛物线上三点,若
为该抛物线上三点,若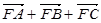 =0,则
=0,则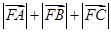 的值为
的值为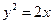 的焦点作直线交抛物线于
的焦点作直线交抛物线于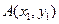 、
、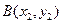 两点,若
两点,若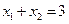 ,则
,则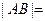 .
.
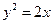 的焦点为F,
的焦点为F,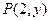 在抛物线上,则|PF|= .
在抛物线上,则|PF|= .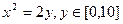 ,在杯内放入一个清洁球,要求清洁球能擦净酒杯的最底部(如图),则清洁球的最大半径为
,在杯内放入一个清洁球,要求清洁球能擦净酒杯的最底部(如图),则清洁球的最大半径为 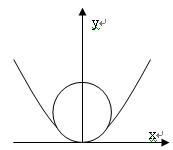
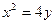 的焦点为F,准线与y轴的交点为M,N为抛物线上的一点,且
的焦点为F,准线与y轴的交点为M,N为抛物线上的一点,且 。
。