题目内容
甲、乙两人参加某种选拔测试.在备选的10道题中,甲答对其中每道题的概率都是 ,乙能答对其中的5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,得分最低为0分,至少得15分才能入选.
,乙能答对其中的5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,得分最低为0分,至少得15分才能入选.
(Ⅰ)求乙得分的分布列和数学期望;
(Ⅱ)求甲、乙两人中至少有一人入选的概率.
(Ⅰ)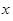 的分布列为
的分布列为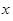
0 15 30 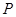
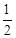

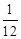
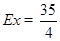 ;(Ⅱ)甲、乙两人中至少有一人入选的概率
;(Ⅱ)甲、乙两人中至少有一人入选的概率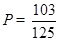 .
.
解析试题分析:(Ⅰ)此题属于答错扣分问题,得分最低为零分,它包括两种情况,一种是三个都答错,一种是三个答对一个,若三个答对两个,此时得分为15分,若三个答对三个,此时得分为30分,故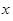 =
=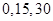 ,计算出各个概率,可得分布列,从而求出数学期望;(Ⅱ)甲、乙两人中至少有一人入选,像这种至少有一问题,常常采用对立事件来解,即甲乙都没入选,分别求出甲乙没入选的概率,从而求出甲、乙两人中至少有一人入选的概率.
,计算出各个概率,可得分布列,从而求出数学期望;(Ⅱ)甲、乙两人中至少有一人入选,像这种至少有一问题,常常采用对立事件来解,即甲乙都没入选,分别求出甲乙没入选的概率,从而求出甲、乙两人中至少有一人入选的概率.
试题解析:(Ⅰ)设乙得分为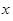 ,则
,则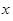 =
=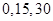 ,
,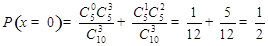 ,
,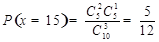 ,
,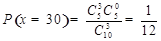
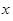 的分布列为
的分布列为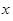
0 15 30 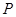
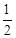

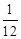
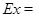
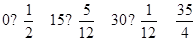 ;
;
(Ⅱ)设“甲入选”为事件A,“乙入选”为事件B,则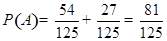 ,
, ,
,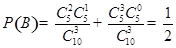 ,
,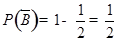 ,所求概率
,所求概率
考点:本小题考查独立事件与对立事件的概率,分布列,数学期望,考查学生的分析问题、解决问题的能力.

练习册系列答案
相关题目
某社团组织 名志愿者利用周末和节假日参加社会公益活动,活动内容是:1、到各社区宣传慰问,倡导文明新风;2、到指定的医院、福利院做义工,帮助那些需要帮助的人.各位志愿者根据各自的实际情况,选择了不同的活动项目,相关的数据如下表所示:
名志愿者利用周末和节假日参加社会公益活动,活动内容是:1、到各社区宣传慰问,倡导文明新风;2、到指定的医院、福利院做义工,帮助那些需要帮助的人.各位志愿者根据各自的实际情况,选择了不同的活动项目,相关的数据如下表所示:
| | 宣传慰问 | 义工 | 总计 |
| 20至40岁 | 11 | 16 | 27 |
| 大于40岁 | 15 | 8 | 23 |
| 总计 | 26 | 24 | 50 |
(2) 上述抽取的6名志愿者中任取2名,求选到的志愿者年龄大于40岁的人数的数学期望.
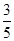 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是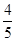 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用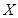 表示张同学答对题的个数,求
表示张同学答对题的个数,求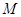 名学生作为样本,得到这
名学生作为样本,得到这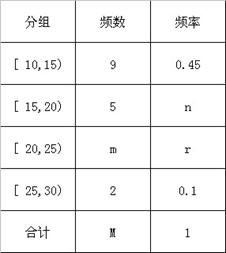
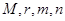 的值;
的值; 次的学生中任选
次的学生中任选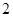 人,求至少一人参加社区服务次数在区间
人,求至少一人参加社区服务次数在区间 内的概率.
内的概率.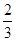 .
.