题目内容
一个口袋中有红球3个,白球4个.
(Ⅰ)从中不放回地摸球,每次摸2个,摸到的2个球中至少有1个红球则中奖,求摸2次恰好第2次中奖的概率;
(Ⅱ)每次同时摸2个,并放回,摸到的2个球中至少有1个红球则中奖,连续摸4次,求中奖次数X的数学期望E(X).
(Ⅰ)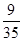 ;(Ⅱ)
;(Ⅱ)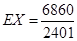 ,
,
解析试题分析:(Ⅰ)利用排列组合、古典概率公式可求;(Ⅱ)按照分布列的取值情况求对应的概率即可.
试题解析:(Ⅰ) 设“摸2次恰好第2次中奖”为事件A,则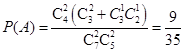
所以,摸2次恰好第2次中奖的概率为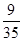 . 5分
. 5分
(Ⅱ) 设“每次同时摸2个,恰好中奖”为事件B,则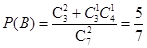
随机变量X的所有可能取值为1,2,3,4. 6分 ,
, 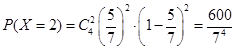 ,
,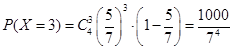 ,
, 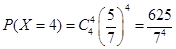 , 10分
, 10分
所以随机变量X的分布列是
随机变量X的数学期望X 1 2 3 4 P 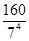
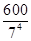
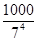
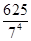
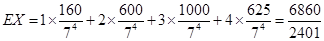 . 14分
. 14分
考点:组合公式、概率,分布列,期望

练习册系列答案
相关题目
在一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于 分为优秀,
分为优秀, 分以下为非优秀,统计成绩后,得到如下的
分以下为非优秀,统计成绩后,得到如下的 列联表,且已知在甲、乙两个文科班全部
列联表,且已知在甲、乙两个文科班全部 人中随机抽取人为优秀的概率为
人中随机抽取人为优秀的概率为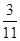 .
.
| | 优秀 | 非优秀 | 合计 |
| 甲班 |  | | |
| 乙班 | |  | |
| 合计 | | |  |
(2)根据列联表的数据,能否有
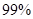 的把握认为成绩与班级有关系?
的把握认为成绩与班级有关系?(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的
 名学生从
名学生从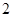 到
到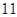 进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号,试求抽到
进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号,试求抽到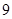 号或
号或 号的概率.
号的概率. 为了对某课题进行研究,用分层抽样方法从三所科研单位A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人):
| 科研单位 | 相关人数 | 抽取人数 |
| A | 16 | 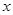 |
| B | 12 | 3 |
| C | 8 | 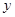 |
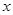 与
与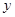 的值;
的值;(2)若从科研单位A、C抽取的人中选2人作专题发言,求这2人都来自科研单位A的概率.
随着经济的发展,人们生活水平的提高,中学生的营养与健康问题越来越得到学校与家长的重视. 从学生体检评价报告单了解到某校3000名学生的体重发育评价情况,得右表:
| | 偏瘦 | 正常 | 肥胖 |
| 女生(人) | 300 | 865 |  |
| 男生(人) | 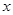 | 885 | 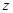 |
(Ⅰ)求
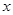 的值;
的值;(Ⅱ)若用分层抽样的方法,从这批学生中随机抽取60名,问应在肥胖学生中抽出多少名?
(Ⅲ)已知
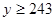 ,
,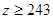 ,求肥胖学生中男生不少于女生的概率.
,求肥胖学生中男生不少于女生的概率.  、
、 、
、 三组测试项目供参考人员选择,甲、乙、丙、丁、戊五人参加招聘,其中甲、乙两人各自独立参加
三组测试项目供参考人员选择,甲、乙、丙、丁、戊五人参加招聘,其中甲、乙两人各自独立参加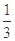 ,丙、丁两人各自通过测试的概率均为
,丙、丁两人各自通过测试的概率均为 .戊参加
.戊参加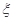 ,求
,求 只,其中有
只,其中有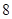 只合格品,
只合格品, 只次品。
只次品。 次,每次取一只灯泡,求
次,每次取一只灯泡,求 的分布列和数学期望.
的分布列和数学期望. ,乙能答对其中的5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,得分最低为0分,至少得15分才能入选.
,乙能答对其中的5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,得分最低为0分,至少得15分才能入选. .
.