题目内容
在半径为1的圆周上任取三点,连接成三角形,这个三角形是锐角三角形的概率是多少?
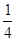
解析试题分析:当基本事件等可能,且个数无限时,考虑几何概型求概率(长度的比值、面积的比值、体积的比值),①若题中涉及一个变量转化为长度比值;②若涉及两个变量,利用平面直角坐标系构建二维平面区域,转为为面积的比值,本题记事件 “三点组成锐角三角形”,可先固定
“三点组成锐角三角形”,可先固定 点,不妨设
点,不妨设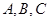 三点在圆上按逆时针排列,如图所示,利用同弧所对的圆心角和圆周角的关系,当
三点在圆上按逆时针排列,如图所示,利用同弧所对的圆心角和圆周角的关系,当 时,
时,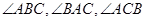 都小于
都小于 则事件
则事件 发生,这里涉及三个变量,但只要设出其中两个变量,第三个变量可以表示出来,设
发生,这里涉及三个变量,但只要设出其中两个变量,第三个变量可以表示出来,设 在平面直角坐标系下,将
在平面直角坐标系下,将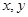 作为点的横坐标与纵坐标,这样所有的点
作为点的横坐标与纵坐标,这样所有的点 构成了平面图形,这样问题就转化为测度为面积的二维几何概型.
构成了平面图形,这样问题就转化为测度为面积的二维几何概型.
试题解析:如图①,按照逆时针方向依次标记三点为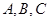 .设弧
.设弧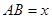 ,弧
,弧 ,弧
,弧

依题意,所有可能的结果构成平面区域: 3分
3分
事件 “三点组成锐角三角形”构成的平面区域:
“三点组成锐角三角形”构成的平面区域:
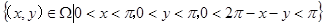 6分
6分 8分
8分 10分
10分
所以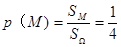 12分
12分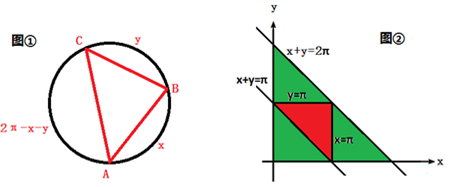

考点:几何概型.

 天天练口算系列答案
天天练口算系列答案某公司欲招聘员工,从1000名报名者中筛选200名参加笔试,按笔试成绩择优取50名面试,再从面试对象中聘用20名员工.
(Ⅰ)求每个报名者能被聘用的概率;
(Ⅱ)随机调查了24名笔试者的成绩如下表所示:
| 分数段 | [60,65) | [65,70) | [70,75) | [75,80) | [80,85) | [85,90) |
| 人数 | 1 | 2 | 6 | 9 | 5 | 1 |
(Ⅲ)公司从聘用的四男
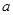 、
、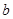 、
、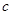 、
、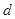 和二女
和二女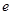 、
、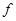 中选派两人参加某项培训,则选派结果为一男一女的概率是多少?
中选派两人参加某项培训,则选派结果为一男一女的概率是多少? 有一种密码,明文是由三个字符组成,密码是由明文对应的五个数字组成,编码规则如下表:明文由表中每一排取一个字符组成且第一排取的字符放在第一位,第二排取的字符放在第二位,第三排取的字符放在第三位,对应的密码由明文对应的数字按相同的次序排列组成.
| 第一排 | 明文字符 | A | B | C | D |
| 密码字符 | 11 | 12 | 13 | 14 | |
| 第二排 | 明文字符 | E | F | G | H |
| 密码字符 | 21 | 22 | 23 | 24 | |
| 第三排 | 明文字符 | M | N | P | Q |
| 密码字符 | 1 | 2 | 3 | 4 |
(1)求
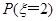 ;
;(2)求随机变量
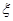 的分布列和数学期望.
的分布列和数学期望. (本小题满分12分)有一种密码,明文是由三个字符组成,密码是由明文对应的五个数字组成,编码规则如下表:明文由表中每一排取一个字符组成,且第一排取的字符放在第一位,第二排取的字符放在第二位,第三排取的字符放在第三位,对应的密码由明文对应的数字按相同的次序排成一排组成.
| 第一排 | 明文字符 | A | B | C | D |
| 密码字符 | 11 | 12 | 13 | 14 | |
| 第二排 | 明文字符 | E | F | G | H |
| 密码字符 | 21 | 22 | 23 | 24 | |
| 第三排 | 明文字符 | M | N | P | Q |
| 密码字符 | 1 | 2 | 3 | 4 |
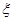 表示密码中不同数字的个数.
表示密码中不同数字的个数.(Ⅰ)求
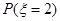 ; (Ⅱ)求随机变量
; (Ⅱ)求随机变量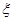 的分布列和它的数学期望.
的分布列和它的数学期望. 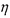 的方差是多少?
的方差是多少?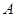 到
到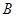 有6条网线,数字表示该网线单位时间内可以通过的最大信息量,现从中任取3条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息之和为
有6条网线,数字表示该网线单位时间内可以通过的最大信息量,现从中任取3条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息之和为 .
.
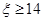 时,线路信息畅通,求线路信息畅通的概率;
时,线路信息畅通,求线路信息畅通的概率; 、
、 、
、 三组测试项目供参考人员选择,甲、乙、丙、丁、戊五人参加招聘,其中甲、乙两人各自独立参加
三组测试项目供参考人员选择,甲、乙、丙、丁、戊五人参加招聘,其中甲、乙两人各自独立参加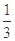 ,丙、丁两人各自通过测试的概率均为
,丙、丁两人各自通过测试的概率均为 .戊参加
.戊参加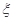 ,求
,求 户家庭,分别调查了他们在政府动员前后三个月的月平均用水量(单位:吨),将所得数据分组,画出频率分布直方图(如图所示)
户家庭,分别调查了他们在政府动员前后三个月的月平均用水量(单位:吨),将所得数据分组,画出频率分布直方图(如图所示)

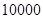 户,在政府进行节水动员前平均每月用水量是
户,在政府进行节水动员前平均每月用水量是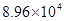 吨,请估计该小区在政府动员后比动员前平均每月节约用水多少吨;
吨,请估计该小区在政府动员后比动员前平均每月节约用水多少吨;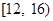 范围内的家庭中选出
范围内的家庭中选出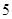 户作为采访对象,其中在
户作为采访对象,其中在 内的抽到
内的抽到 户,求
户,求 ,乙能答对其中的5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,得分最低为0分,至少得15分才能入选.
,乙能答对其中的5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,得分最低为0分,至少得15分才能入选.