题目内容
现有10道题,其中6道甲类题,4道乙类题,张同学从中任取3道题解答.
(I)求张同学至少取到1道乙类题的概率;
(II)已知所取的3道题中有2道甲类题,1道乙类题.设张同学答对甲类题的概率都是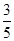 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是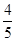 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用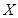 表示张同学答对题的个数,求
表示张同学答对题的个数,求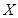 的分布列和数学期望.
的分布列和数学期望.
(Ⅰ) ;(Ⅱ)分布列见解析,
;(Ⅱ)分布列见解析, .
.
解析试题分析:(Ⅰ)先求出张同学取到的题中没有乙类题的概率是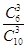 ,则张同学至少取到1道乙类题的概率为:
,则张同学至少取到1道乙类题的概率为: ;(Ⅱ)
;(Ⅱ) 的所有可能的取值为:
的所有可能的取值为: ,分别求出
,分别求出 在每种取值下的概率:当
在每种取值下的概率:当 时,全部答错,
时,全部答错, ;当
;当 时,只答对一道甲类题或只答对一道乙类题,
时,只答对一道甲类题或只答对一道乙类题, ;当
;当 时,答对两道甲类题或答对一道甲类题和一道乙类题,
时,答对两道甲类题或答对一道甲类题和一道乙类题, ;当
;当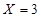 时,三道题都答对,
时,三道题都答对, .列出分布列,根据
.列出分布列,根据 求出随机变量
求出随机变量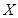 的数学期望.
的数学期望.
试题解析:(Ⅰ)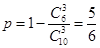
(Ⅱ)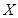 的所有可能的取值为:
的所有可能的取值为: ,
,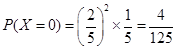 ,
,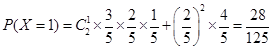 ,
,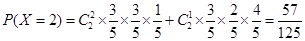 ,
,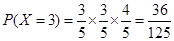 .
.
∴X的分布列为:
∴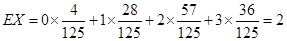 .
.
考点:1.相互独立事件的概率;2.离散型随机变量的及其应用;3.古典概型;4.分布列和期望

练习册系列答案
相关题目
为了解某班学生喜爱打篮球是否与性别有关,对本班48人进行了问卷调查得到了如下的2×2列联表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 6 | |
| 女生 | 10 | | |
| 合计 | | | 48 |
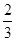 .
.(1)请将上面的2×2列联表补充完整(不用写计算过程);
(2)你是否有95%的把握认为喜爱打篮球与性别有关?说明你的理由;
(3)现从女生中抽取2人进一步调查,设其中喜爱打篮球的女生人数为X,求X的分布列与数学期望.
下面的临界值表供参考:
| P(χ2≥x0)或 P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| x0(或k0) | 2.706 | 3.841 | 6.635 | 7.879 |
(参考公式)χ2=
 ,其中n=n11+n12+n21+n22或K2=
,其中n=n11+n12+n21+n22或K2=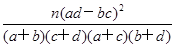 ,其中n=a+b+c+d)
,其中n=a+b+c+d) 为了参加2013年东亚运动会,从四支较强的排球队中选出18人组成女子排球国家队,队员来源如下表:
| 对别 | 北京 | 上海 | 天津 | 广州 |
| 人数 | 4 | 6 | 3 | 5 |
(2)比赛结束后,若要求选出两名队员代表发言,设其中来自北京的人数为
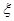 ,求随机变量
,求随机变量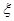 的分布列,及数学期望.
的分布列,及数学期望. 某公司欲招聘员工,从1000名报名者中筛选200名参加笔试,按笔试成绩择优取50名面试,再从面试对象中聘用20名员工.
(Ⅰ)求每个报名者能被聘用的概率;
(Ⅱ)随机调查了24名笔试者的成绩如下表所示:
| 分数段 | [60,65) | [65,70) | [70,75) | [75,80) | [80,85) | [85,90) |
| 人数 | 1 | 2 | 6 | 9 | 5 | 1 |
(Ⅲ)公司从聘用的四男
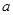 、
、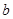 、
、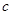 、
、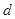 和二女
和二女 、
、 中选派两人参加某项培训,则选派结果为一男一女的概率是多少?
中选派两人参加某项培训,则选派结果为一男一女的概率是多少? 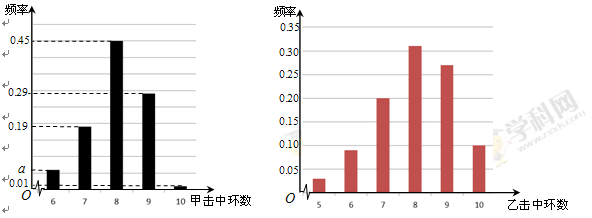
 的值;
的值;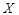 的分布列及数学期望(频率当作概率使用);
的分布列及数学期望(频率当作概率使用);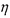 的方差是多少?
的方差是多少? 就去打球;若
就去打球;若 就去唱歌;若
就去唱歌;若 就去下棋.
就去下棋.
 ,乙能答对其中的5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,得分最低为0分,至少得15分才能入选.
,乙能答对其中的5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,得分最低为0分,至少得15分才能入选.