题目内容
现有A,B两球队进行友谊比赛,设A队在每局比赛中获胜的概率都是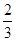 .
.
(Ⅰ)若比赛6局,求A队至多获胜4局的概率;
(Ⅱ)若采用“五局三胜”制,求比赛局数ξ的分布列和数学期望.
(Ⅰ)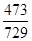 ;(Ⅱ)E(ξ)=
;(Ⅱ)E(ξ)=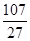 .
.
解析试题分析:(Ⅰ)利用“正难则反”的思路来求;(Ⅱ)按照分布列的取值情况求对应的概率即可.
试题解析:(Ⅰ) 记“比赛6局,A队至多获胜4局”为事件A,
则P(A)=1-[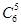 (
(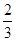 )5(1-
)5(1-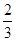 )+
)+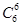 (
(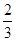 )6]=1-
)6]=1-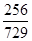 =
=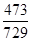 .
.
故A队至多获胜4局的概率为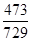 . 4分
. 4分
(Ⅱ)由题意可知,ξ的可能取值为3,4,5.
P(ξ=3)=(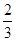 )3+(
)3+(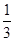 )3=
)3=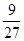 =
=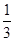 ,
,
P(ξ=4)=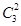 (
(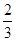 )2×
)2×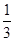 ×
×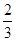 +
+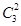 (
(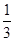 )2×
)2×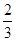 ×
×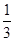 =
=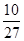 ,
,
P(ξ=5)= (
(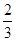 )2(
)2(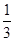 )2=
)2= .
.
∴ξ的分布列为:
∴E(ξ)=3×ξ 3 4 5 P 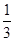
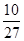

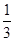 +4×
+4×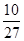 +5×
+5× =
=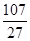 . 12分
. 12分
考点:排列组合,分布列,期望.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
有一种密码,明文是由三个字符组成,密码是由明文对应的五个数字组成,编码规则如下表:明文由表中每一排取一个字符组成且第一排取的字符放在第一位,第二排取的字符放在第二位,第三排取的字符放在第三位,对应的密码由明文对应的数字按相同的次序排列组成.
| 第一排 | 明文字符 | A | B | C | D |
| 密码字符 | 11 | 12 | 13 | 14 | |
| 第二排 | 明文字符 | E | F | G | H |
| 密码字符 | 21 | 22 | 23 | 24 | |
| 第三排 | 明文字符 | M | N | P | Q |
| 密码字符 | 1 | 2 | 3 | 4 |
(1)求
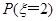 ;
;(2)求随机变量
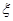 的分布列和数学期望.
的分布列和数学期望. 为了对某课题进行研究,用分层抽样方法从三所科研单位A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人):
| 科研单位 | 相关人数 | 抽取人数 |
| A | 16 | 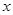 |
| B | 12 | 3 |
| C | 8 | 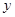 |
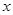 与
与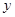 的值;
的值;(2)若从科研单位A、C抽取的人中选2人作专题发言,求这2人都来自科研单位A的概率.
 就去打球;若
就去打球;若 就去唱歌;若
就去唱歌;若 就去下棋.
就去下棋.
 、
、 、
、 三组测试项目供参考人员选择,甲、乙、丙、丁、戊五人参加招聘,其中甲、乙两人各自独立参加
三组测试项目供参考人员选择,甲、乙、丙、丁、戊五人参加招聘,其中甲、乙两人各自独立参加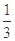 ,丙、丁两人各自通过测试的概率均为
,丙、丁两人各自通过测试的概率均为 .戊参加
.戊参加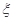 ,求
,求 ,乙能答对其中的5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,得分最低为0分,至少得15分才能入选.
,乙能答对其中的5道题.规定每次考试都从备选的10道题中随机抽出3道题进行测试,答对一题加10分,答错一题(不答视为答错)减5分,得分最低为0分,至少得15分才能入选. .
. 和获得等级不是
和获得等级不是 、
、 、
、 ,物理、化学、生物获得等级不是
,物理、化学、生物获得等级不是 、
、 、
、 .
. );
);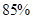 ,并说明理由.
,并说明理由. 箱中有3个黑球,6个白球,每个球被取到的概率相同,
箱中有3个黑球,6个白球,每个球被取到的概率相同,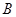 箱中没有球.我们把从
箱中没有球.我们把从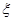 ,求
,求