题目内容
14.已知等差数列{an}和{bn}的前n项和分别为Sn和Tn,且$\frac{{S}_{n}}{{T}_{n}}$=$\frac{7n+43}{n+4}$,则$\frac{{a}_{6}}{{b}_{6}}$为( )| A. | 7 | B. | 8 | C. | 5 | D. | 6 |
分析 由等差数列的求和公式和性质可得$\frac{{a}_{6}}{{b}_{6}}$=$\frac{{S}_{11}}{{T}_{11}}$,代值计算可得.
解答 解:由等差数列的求和公式和性质可得:
$\frac{{a}_{6}}{{b}_{6}}$=$\frac{2{a}_{6}}{2{b}_{6}}$=$\frac{{a}_{1}+{a}_{11}}{{b}_{1}+{b}_{11}}$=$\frac{\frac{11({a}_{1}+{a}_{11})}{2}}{\frac{11({b}_{1}+{b}_{11})}{2}}$
=$\frac{{S}_{11}}{{T}_{11}}$=$\frac{7×11+43}{11+4}$=8
故选:B
点评 本题考查等差数列的性质和求和公式,属基础题.

练习册系列答案
相关题目
19.函数f(x)=4x2-kx-8在区间(-∞,5]上是减函数,则实数k的取值范围是( )
| A. | k≥40 | B. | k≤40 | C. | k≥5 | D. | k≤5 |
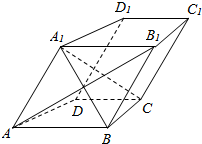 如图,在四棱柱ABCD-A1B1C1D1中,AB∥C1D1,AB1⊥BC,且AA1=AB.
如图,在四棱柱ABCD-A1B1C1D1中,AB∥C1D1,AB1⊥BC,且AA1=AB.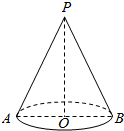 如图所示,圆锥的母线长l,轴截面PAB内,∠PAO=60°,
如图所示,圆锥的母线长l,轴截面PAB内,∠PAO=60°,