题目内容
2．已知函数y=2x-x2+m的最大值为5，则m=4．分析 二次函数的最大值即为顶点纵坐标的值，根据顶点纵坐标公式，列方程求解．
解答 解：二次函数y=2x-x2+m的顶点纵坐标为 $\frac{-4m-{2}^{2}}{-4}$，
依题意，得$\frac{-4m-{2}^{2}}{-4}=5$，
解得m=4．
故答案为：4．
点评 本题考查了二次函数解析式顶点坐标公式的运用．二次函数y=ax2+bx+c的顶点坐标为（-$\frac{b}{2a}$，$\frac{4ac-{b}^{2}}{4a}$）．
练习册系列答案
习题精选系列答案
相关题目
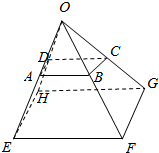已知O、A、B、C、D、F、F、G、H为空间9个点（如图），并且$\overrightarrow{OE}$=k$\overrightarrow{OA}$，$\overrightarrow{OF}$=k$\overrightarrow{OB}$，$\overrightarrow{OH}$=k$\overrightarrow{OD}$，$\overrightarrow{AC}$=$\overrightarrow{AD}$+m$\overrightarrow{AB}$，$\overrightarrow{EG}$=$\overrightarrow{EH}$+m$\overrightarrow{EF}$．求证：
10．下列命题正确的是（ ）
| A． | 负角一定在第四象限 | B． | 钝角比第三象限的角小 | ||
| C． | 坐标轴上的角都是正角 | D． | 锐角都是第一象限的角 |
7．已知数列{an}满足a${\;}_{n+1}^{2}$=anan+2（n∈N*），且32a8-a3=0，记Sn是数列{an}的前n项和，则$\frac{{S}_{6}}{{a}_{1}-{S}_{3}}$的值为（ ）
| A． | $\frac{21}{8}$ | B． | -9 | C． | 9 | D． | -$\frac{21}{8}$ |